设函数f(x)=$\left\{\begin{array}{l}{{x}^{2}.x≤1}\\{{2}^{-x}.x＞1}\end{array}\right.$.则fA．$\frac{1}{16}$B．16C．$\frac{1}{4}$D．4 题目和参考答案——青夏教育精英家教网—

题目内容

15．设函数f（x）=$\left\{\begin{array}{l}{{x}^{2}，x≤1}\\{{2}^{-x}，x＞1}\end{array}\right.$，则f（f（2））=（　　）

A．

$\frac{1}{16}$

B．

C．

$\frac{1}{4}$

D．

分析先求出f（2）=2^-2=$\frac{1}{4}$，从而f（f（2））=f（$\frac{1}{4}$），由此能求出结果．

解答解：∵f（x）=$\left\{\begin{array}{l}{{x}^{2}，x≤1}\\{{2}^{-x}，x＞1}\end{array}\right.$，
∴f（2）=2^-2=$\frac{1}{4}$，
f（f（2））=f（$\frac{1}{4}$）=（$\frac{1}{4}$）²=$\frac{1}{16}$．
故选：A．

点评本题考查函数值的求法，是基础题，解题时要认真审题，注意函数性质的合理运用．

练习册系列答案

中考热点作家作品阅读系列答案

Short Stories for Comprehension妙语短篇系列答案

6．设某等腰三角形的底角为α，顶角为β，且cosβ=$\frac{3}{5}$．
（Ⅰ）求sinα的值；
（Ⅱ）若函数f（x）=tanx在[-$\frac{π}{3}$，α]上的值域与函数g（x）=2sin（2x-$\frac{π}{3}$）在[0，m]上的值域相同，求m的取值范围．

3．已知a=2^0.3，b=log_0.23，c=log₃2，则a，b，c的大小关系是（　　）

10．已知函数f（x）=$\left\{\begin{array}{l}{a{x}^{3}，x＞0}\\{cosx，-\frac{π}{2}＜x＜0}\end{array}\right.$（a∈R），若f（f（-$\frac{π}{3}$））=1，则a的值为8．

20．记[x]表示不超过x的最大整数，如[1.2]=1，[0.5]=0，则方程[x]-x=lnx的实数根的个数为（　　）

7．

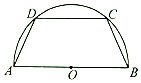如图，有一块半径为2的半圆形钢板，计划剪裁成等腰梯形ABCD的形状，它的下底AB是⊙O的直径，上底CD的端点在圆周上．设∠DAB=θ（0＜θ＜$\frac{π}{2}$），L为等腰梯形ABCD的周长．
（1）求周长L与θ的函数解析式；
（2）试问周长L是否存在最大值？若存在，请求出最大值，并指出此时θ的大小；若不存在，请说明理由．

4．

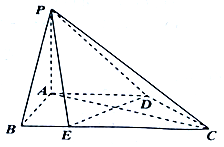如图，在四棱锥P-ABCD中，底面ABCD为直角梯形，AB⊥AD，AD∥BC，AD=$\frac{1}{2}$BC=2，E在BC上，且BE=$\frac{1}{2}$AB=1，侧棱PA⊥平面ABCD．
（1）求证：平面PDE⊥平面PAC；
（2）若△PAB为等腰直角三角形．
（i）求直线PE与平面PAC所成角的正弦值；
（ii）求二面角A-PC-D的余弦值．

5．在（x-2）¹⁰展开式中，二项式系数的最大值为 a，含x⁷项的系数为b，则$\frac{b}{a}$=（　　）

试题分类