题目内容
15.已知圆C:x2+y2=4,则过圆上点$(1,\sqrt{3})$的切线方程是$x+\sqrt{3}y-4=0$.分析 直接利用圆上的点的切线方程,求出即可.
解答 解:因为(1,$\sqrt{3}$)是圆x2+y2=4上的点,
所以它的切线方程为:x+$\sqrt{3}$y=4,
即$x+\sqrt{3}y-4=0$.
故答案为$x+\sqrt{3}y-4=0$.
点评 本题考查圆的切线方程,判断点在圆上是解题的关键.圆上的点(x0,y0)的切线方程为:xx0+yy0=R2,值得注意圆的切线方程的应用.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案
相关题目
6.函数y=$\frac{sinx}{|sinx|}$+$\frac{|cosx|}{cosx}$+$\frac{tanx}{|tanx|}$的值域是( )
| A. | {1} | B. | {1,3} | C. | {-1} | D. | {-1,3} |
5.已知抛物线y2=2px(p>0)经过点A(1,$\frac{1}{2}$),则它的准线方程为( )
| A. | x=-$\frac{1}{32}$ | B. | x=-$\frac{1}{16}$ | C. | y=-$\frac{1}{32}$ | D. | y=-$\frac{1}{16}$ |
 如图,在四棱锥S-ABCD中,底面ABCD是棱长为2的正方形,侧棱$SD=2,SA=2\sqrt{2}$,∠SDC=120°.
如图,在四棱锥S-ABCD中,底面ABCD是棱长为2的正方形,侧棱$SD=2,SA=2\sqrt{2}$,∠SDC=120°.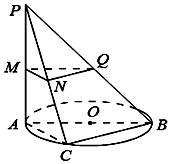 如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.
如图,⊙O在平面α内,AB是⊙O的直径,PA⊥平面α,C为圆周上不同于A、B的任意一点,M,N,Q分别是PA,PC,PB的中点.