题目内容
14.已知cosθ>0,tan(θ+$\frac{π}{4}$)=$\frac{1}{3}$,则θ在( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 由两角和的正切公式化简tan(θ+$\frac{π}{4}$)=$\frac{1}{3}$,求出tanθ的值,结合条件和三角函数值的符号判断出θ所在的象限.
解答 解:由题意得,tan(θ+$\frac{π}{4}$)=$\frac{1}{3}$,
所以$\frac{tan\frac{π}{4}+tanθ}{1-tan\frac{π}{4}tanθ}$=$\frac{1}{3}$,即$\frac{1+tanθ}{1-tanθ}=\frac{1}{3}$,
解得tanθ=$-\frac{1}{2}$<0,则θ在第二或四象限,
由cosθ>0得,θ在第一或四象限,
所以θ在第四象限,
故选:D.
点评 本题考查了两角和的正切公式,以及三角函数值的符号,属于基础题.

练习册系列答案
相关题目
5.已知抛物线y2=2px(p>0)经过点A(1,$\frac{1}{2}$),则它的准线方程为( )
| A. | x=-$\frac{1}{32}$ | B. | x=-$\frac{1}{16}$ | C. | y=-$\frac{1}{32}$ | D. | y=-$\frac{1}{16}$ |
3.已知a=20.3,b=log0.23,c=log32,则a,b,c的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | b<a<c | D. | b<c<a |
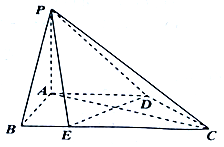 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=$\frac{1}{2}$BC=2,E在BC上,且BE=$\frac{1}{2}$AB=1,侧棱PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AB⊥AD,AD∥BC,AD=$\frac{1}{2}$BC=2,E在BC上,且BE=$\frac{1}{2}$AB=1,侧棱PA⊥平面ABCD.