题目内容
试比较
-1和
的大小．
| 1+a |
| a |
考点：不等式比较大小
专题：不等式的解法及应用
分析：平方作差即可得出．
解答：
解：∵a≥0，
∴
-1≥0．
∵(
-1)2-(
)2
=1+a+1-2
-a
=2(1-
)．
∵a≥0，∴1≤
，
∴
-1≤
．
∴
| 1+a |
∵(
| 1+a |
| a |
=1+a+1-2
| 1+a |
=2(1-
| 1+a |
∵a≥0，∴1≤
| 1+a |
∴
| 1+a |
| a |
点评：本题考查了“平方作差法”比较数的大小，考查了计算能力，属于基础题．
练习册系列答案
相关题目
若x2cosα+y2sinα+1=0（α∈（0，2π））表示一个圆，则（ ）
A、0＜α＜
| ||
B、π＜α＜
| ||
C、α=
| ||
D、α=
|
已知i是虚数单位，若z（1+3i）=i，则z的虚部为（ ）
A、
| ||
B、-
| ||
C、
| ||
D、-
|
已知集合A={x|x2≥1}，B={x|y=
}，则A∩∁RB=（ ）
| 1-log2x |
| A、（2，+∞） |
| B、（-∞，-1]∪（2，+∞） |
| C、（-∞，-1）∪（2，+∞） |
| D、[-1，0]∪[2，+∞） |
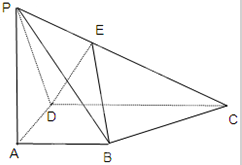如图，PA⊥平面ABCD，底面ABCD是直角梯形，AB⊥AD，AB=AD，CD=2AB，E为PC中点．若PB与平面ABCD所成的角为45°
已知P是抛物线x2=2py（p＞0）上的动点，P到抛物线焦点的距离比到x轴的距离大1．