题目内容
18．已知集合A={x||x-1|＜2}，B={x|log2x＜3}，则A∩B=（ ）| A． | （-1，3） | B． | （0，3） | C． | （0，8） | D． | （-1，8） |
分析 分别求出集合A和B，由此能出A∩B．
解答 解：∵集合A={x||x-1|＜2}={x|-1＜x＜3}，
B={x|log2x＜3}={x|0＜x＜8}，
∴A∩B={x|0＜x＜3}=（0，3）．
故选：B．
点评 本题考查交集的求法，是基础题，解题时要认真审题，注意交集的性质的合理运用．
练习册系列答案
相关题目
6．函数$f（x）=\frac{1}{lg（x+1）}+\sqrt{2-x}$的定义域为（ ）
| A． | （-1，0）∪（0，2] | B． | [-2，0）∪（0，2] | C． | [-2，2] | D． | （-1，2] |
3．
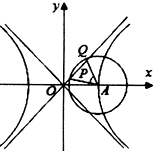如图，已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P、Q，若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$，则双曲线C的离心率为（ ）
如图，已知双曲线$C：\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（{a＞0，b＞0}）$的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的某渐近线交于两点P、Q，若∠PAQ=60°且$\overrightarrow{OQ}$=4$\overrightarrow{OP}$，则双曲线C的离心率为（ ）| A． | $\frac{{2\sqrt{13}}}{5}$ | B． | $\frac{{\sqrt{7}}}{2}$ | C． | $\frac{{2\sqrt{39}}}{9}$ | D． | $\sqrt{3}$ |