题目内容
8.定义在R上的奇函数f(x)满足:当x>0时,f(x)=2x-1,则满足$f(x)<\frac{3}{2}x$的实数x的取值范围为(-∞,-2)∪(0,2).分析 先求出x<0时函数f(x)的解析式,画出f(x)以及y=$\frac{3}{2}$x的图象,数形结合求得满足$f(x)<\frac{3}{2}x$的实数x的取值范围.
解答 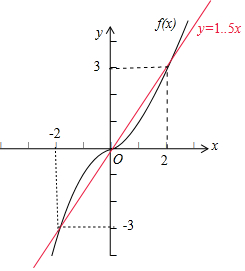 解:定义在R上的奇函数f(x)满足:当x>0时,f(x)=2x-1,
解:定义在R上的奇函数f(x)满足:当x>0时,f(x)=2x-1,
设x<0,则-x>0,∴f(-x)=2-x-1=-f(x),∴f(x)=1-2-x,
令f(x)=$\frac{3}{2}$x,即$\left\{\begin{array}{l}{x>0}\\{{2}^{x}-1=\frac{3}{2}x}\end{array}\right.$,或$\left\{\begin{array}{l}{x<0}\\{1{-2}^{-x}=\frac{3}{2}x}\end{array}\right.$,或x=0,
求得x=2,x=0,x=-2,如图所示:
∴满足$f(x)<\frac{3}{2}x$的实数x的取值范围为 (-∞,-2)∪(0,2),
故答案为:(-∞,-2)∪(0,2).
点评 本题主要考查函数的奇偶性的应用,函数的图象,属于中档题.

练习册系列答案
相关题目
18.已知集合A={x||x-1|<2},B={x|log2x<3},则A∩B=( )
| A. | (-1,3) | B. | (0,3) | C. | (0,8) | D. | (-1,8) |
19.已知函数$f(x)={({\frac{1}{2}})^x}-1-{log_2}x$,若x0是方程f(x)=0的根,则x0∈( )
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | $({1,\frac{3}{2}})$ | D. | $({\frac{3}{2},2})$ |
16.若函数f(x)满足f(x-1)=x2+1,则f(-1)=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
3.已知函数y=f(x)的图象如图所示,则函数y=f(6x)的零点个数为( )


| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
17.函数$y=\frac{1}{x-2}+lg({x+1})$的定义域是( )
| A. | A(-1,+∞) | B. | (-1,2)∪(2,+∞) | C. | (-1,2) | D. | (2,+∞) |
18.为了得到y=cos2x,只需要将y=sin(2x+$\frac{π}{3}$)作如下变换( )
| A. | 向右平移$\frac{π}{3}$个单位 | B. | 向右平移$\frac{π}{6}$个单位 | ||
| C. | 向左平移$\frac{π}{12}$个单位 | D. | 向右平移$\frac{π}{12}$个单位 |