题目内容
7.已知f(x)的定义域为[-1,1],则函数$g(x)=\frac{1}{{ln({x+1})}}+f({2x})$的定义域为$[-\frac{1}{2},0)∪(0,\frac{1}{2}]$.分析 由f(x)的定义域求出f(2x)的定义域,再与分母中对数式的真数大于0且不等于1联立得答案.
解答 解:∵f(x)的定义域为[-1,1],
∴由$\left\{\begin{array}{l}{x+1>0}\\{x+1≠1}\\{-1≤2x≤1}\end{array}\right.$,解得$-\frac{1}{2}≤x≤\frac{1}{2}$且x≠0.
∴函数$g(x)=\frac{1}{{ln({x+1})}}+f({2x})$的定义域为$[-\frac{1}{2},0)∪(0,\frac{1}{2}]$.
故答案为:$[-\frac{1}{2},0)∪(0,\frac{1}{2}]$.
点评 本题考查函数的定义域及其求法,关键是掌握该类问题的求解方法,是基础题.

练习册系列答案
相关题目
17.已知P(-1,2),过P点且与原点距离最大的直线的方程是( )
| A. | x+2y-5=0 | B. | 2x-y+5=0 | C. | x-2y+5=0 | D. | 2x+y-5=0 |
18.已知集合A={x||x-1|<2},B={x|log2x<3},则A∩B=( )
| A. | (-1,3) | B. | (0,3) | C. | (0,8) | D. | (-1,8) |
15.函数$y=\sqrt{{{log}_{\frac{1}{2}}}(x-1)}$的定义域是( )
| A. | (1,+∞) | B. | (1,2] | C. | (2,+∞) | D. | (-∞,2) |
19.已知函数$f(x)={({\frac{1}{2}})^x}-1-{log_2}x$,若x0是方程f(x)=0的根,则x0∈( )
| A. | $({0,\frac{1}{2}})$ | B. | $({\frac{1}{2},1})$ | C. | $({1,\frac{3}{2}})$ | D. | $({\frac{3}{2},2})$ |
16.若函数f(x)满足f(x-1)=x2+1,则f(-1)=( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
17.函数$y=\frac{1}{x-2}+lg({x+1})$的定义域是( )
| A. | A(-1,+∞) | B. | (-1,2)∪(2,+∞) | C. | (-1,2) | D. | (2,+∞) |
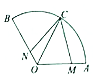 如图,扇形AOB所在圆的半径是1,弧AB的中点为C,动点M,N分别在OA,OB上运动,且满足OM=BN,∠AOB=120°.
如图,扇形AOB所在圆的半径是1,弧AB的中点为C,动点M,N分别在OA,OB上运动,且满足OM=BN,∠AOB=120°.