��Ŀ����
8������ϵ�����������֪��ֱ������ϵxOy�У�����C�IJ�������Ϊ$\left\{\begin{array}{l}x=2+2cos��\\ y=2sin��\end{array}$����Ϊ���������ڼ�����ϵ����ֱ������ϵxOyȡ��ͬ�ij��ȵ�λ������ԭ��OΪ���㣬��x�����Ϊ���ᣩ��ֱ��l�ķ���Ϊ��sin����+$\frac{��}{4}$��=2$\sqrt{2}$����1��������C�ڼ�����ϵ�еķ��̣�
��2����ֱ��l������C�صõ��ҳ���
���� ��1��������C�IJ�����������ͬ�����Ǻ����Ļ�����ϵ��ȥ�����ȣ���Ϊ��ͨ���̣��ٸ���x=��cos�ȣ�y=��sin�ȣ���Ϊ�����귽�̣�
��2����ֱ�ߺ�Բ��ֱ�����귽�����������飬��ý�������꣬�����������ľ��빫ʽ����ҳ���
��� �⣺��1������C����ͨ����Ϊ��x-2��2+y2=4��
��x2+y2-4x=0����$\left\{\begin{array}{l}x=��cos��\\ y=��sin��\end{array}\right.$���뷽��x2+y2-4x=0����æ�=4cos�ȣ�
���ԣ�����C�ļ����귽���Ǧ�=4cos�ȣ�
��2����ֱ��l��ֱ�����귽��Ϊx+y-4=0��
��$\left\{\begin{array}{l}{x^2}+{y^2}-4x=0\\ x+y-4=0\end{array}\right.$��ֱ��l������C�Ľ�������ΪA��2��2����B��4��0����
�����ҳ�|AB|=$\sqrt{��4-2��^{2}+��0-2��^{2}}$=2$\sqrt{2}$��
���� ������Ҫ����Ѳ������̡������귽�̻�Ϊֱ�����귽�̵ķ�������ֱ�ߺ�Բ�Ľ������꣬�����ľ��빫ʽ��Ӧ�ã����ڻ����⣮

��ϰ��ϵ�д�
�����Ŀ
3���輯��A={x|log2��x2-3x����2}��B={x|$\frac{x+3}{2-x}$��0}����A��B=��������
| A�� | ��-1��0�� | B�� | ��-1��2�� | C�� | ��-1��2] | D�� | ��0��2] |
17����֪P��-1��2������P������ԭ���������ֱ�ߵķ����ǣ�������
| A�� | x+2y-5=0 | B�� | 2x-y+5=0 | C�� | x-2y+5=0 | D�� | 2x+y-5=0 |
18����֪����A={x||x-1|��2}��B={x|log2x��3}����A��B=��������
| A�� | ��-1��3�� | B�� | ��0��3�� | C�� | ��0��8�� | D�� | ��-1��8�� |
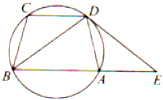 ��ͼ����֪Բ�ϵ��ĵ�A��B��C��D��CD��AB������D��Բ������DE��BA���ӳ��߽���E�㣮
��ͼ����֪Բ�ϵ��ĵ�A��B��C��D��CD��AB������D��Բ������DE��BA���ӳ��߽���E�㣮