题目内容
已知不等式x2+ax+b≤0与2x-
≤1同解（即解集相同），求a、b的值．
| x |
考点：其他不等式的解法
专题：不等式的解法及应用
分析：用换元法，设t=
，把不等式2x-
≤1化为等价的不等式，求出它的解集来，即得不等式x2+ax+b≤0的解集，从而求出a、b的值．
| x |
| x |
解答：
解：设t=
，则t≥0，
∴不等式2x-
≤1可化为2t2-t-1≤0；
解得-
＜t≤1；
又∵t≥0，
∴0≤
≤1，
即0≤x≤1；
∴x2+ax+b≤0的解集为[0，1]；
即方程x2+ax+b=0的解为0，1；
∴a=-1，b=0．
| x |
∴不等式2x-
| x |
解得-
| 1 |
| 2 |
又∵t≥0，
∴0≤
| x |
即0≤x≤1；
∴x2+ax+b≤0的解集为[0，1]；
即方程x2+ax+b=0的解为0，1；
∴a=-1，b=0．
点评：本题考查了不等式的解法与应用问题，解题时应灵活地求出不等式的解集，是基础题．
练习册系列答案
相关题目
设a＞b＞0，则下列不等式成立的是（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
已知函数f （x）在区间[a，b]上单调，且f（a）•f（b）＜0，则函数f（x）的图象与x轴在区间[a，b]内（ ）
| A、至多有一个交点 |
| B、必有唯一个交点 |
| C、至少有一个交点 |
| D、没有交点 |
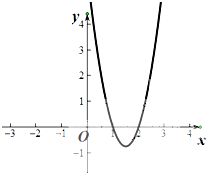已知函数f（x）=ax3+bx2+cx+1的导函数为f′（x），y=f′（x）的图象如图所示