题目内容
方程
=|x+y+2|表示( )
| 2(x+1)2+2(y-1)2 |
| A、椭圆 | B、双曲线 | C、抛物线 | D、圆 |
考点:曲线与方程
专题:圆锥曲线的定义、性质与方程
分析:方程
=|x+y+2|变形为:
=
,由抛物线的定义即可判断出.
| 2(x+1)2+2(y-1)2 |
| (x+1)2+(y-1)2 |
| |x+y+2| | ||
|
解答:
解:方程
=|x+y+2|变形为:
=
,
表示点P(x,y)到定点(-1,1)与定直线的距离相等的点的轨迹,
由抛物线的定义可知:点P的轨迹是抛物线.
故选:C.
| 2(x+1)2+2(y-1)2 |
| (x+1)2+(y-1)2 |
| |x+y+2| | ||
|
表示点P(x,y)到定点(-1,1)与定直线的距离相等的点的轨迹,
由抛物线的定义可知:点P的轨迹是抛物线.
故选:C.
点评:本题考查了抛物线的定义,考查了变形能力与推理能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
为了在运行下面的程序之后输出的y值为16,则输入x的值应该是( )


| A、3或-3 | B、-5 |
| C、-5或5 | D、5或-3 |
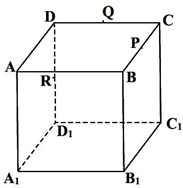 如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题:
如图,正方体ABCD-A1B1C1D1的棱长为2,P,Q,R分别是棱BC,CD,DD1的中点.下列命题: