题目内容
4.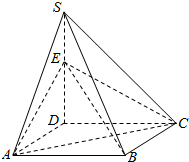 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1).
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1).(Ⅰ)求证:对任意的λ∈(0,1),都有AC⊥BE;
(Ⅱ)若直线DE与平面ACE所成角大小为60°,求λ的值.
分析 (Ⅰ)连接BD,推导出AC⊥BD,由三垂线定理能证明AC⊥BE.
(II)推导出SD⊥CD,CD⊥AD,过点D在平面SAD内作DF⊥AE于F,连接CF,则∠CFD是二面角C-AE-D 的平面角,由此利用直线DE与平面ACE所成角大小为60°,能求出λ.
解答  证明:(Ⅰ)连接BD,由底面是正方形可得AC⊥BD,
证明:(Ⅰ)连接BD,由底面是正方形可得AC⊥BD,
∵SD⊥平面ABCD,∴BD是BE在平面ABCD上的射影,
由三垂线定理得AC⊥BE.
解:(II)∵SD⊥平面ABCD,CD?平面ABCD,∴SD⊥CD.
又底面ABCD是正方形,∴CD⊥AD,
又SD∩AD=D,∴CD⊥平面SAD,
过点D在平面SAD内作DF⊥AE于F,连接CF,则CF⊥AE,
∴∠CFD是二面角C-AE-D 的平面角,
∵直线DE与平面ACE所成角大小为60°,∴∠CFD=60°,
在Rt△ADE中,∵AD=a,DE=λa,AE=a$\sqrt{{λ}^{2}+1}$,
于是,DF=$\frac{AD•DE}{AE}$=$\frac{λa}{\sqrt{{λ}^{2}+1}}$,
在Rt△CDF中,由cot60°=$\frac{DE}{CD}=\frac{λ}{\sqrt{{λ}^{2}+1}}$,
解得$λ=\frac{\sqrt{2}}{2}$.
点评 本题考查线线垂直的证明,考查满足线面角为60°的实数值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
1.已知a3+a-3=a+a-1,则a2等于( )
| A. | 1 | B. | 3$+\sqrt{5}$ | C. | 2$+\sqrt{3}$ | D. | 3$+\sqrt{13}$ |
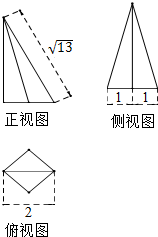
12.如图,已知某个几何体的三视图,根据图中标出的尺寸(单位:mm),可得这个几何体的体积是( )

| A. | 12000000mm3 | B. | 8000000mm3 | C. | 6000000mm3 | D. | 4000000mm3 |
16.i是虚数单位,复数$\frac{(1+i)^{4}}{1-i}$的虚部为( )
| A. | 2i | B. | -2 | C. | i | D. | 1 |
14.已知命题p:?x≥0,2x≥1;命题q:若x>y,则x2>y2.则下列命题为真命题的是( )
| A. | p∧q | B. | p∧¬q | C. | ¬p∧¬q | D. | ¬p∨q |
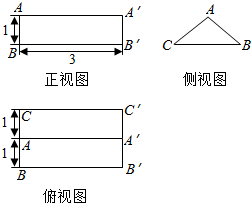 如图是一个几何体的三视图(单位:cm).
如图是一个几何体的三视图(单位:cm).