已知a3+a-3=a+a-1.则a2等于( )A．1B．3$+\sqrt{5}$C．2$+\sqrt{3}$D．3$+\sqrt{13}$ 题目和参考答案——青夏教育精英家教网—

题目内容

1．已知a³+a^-3=a+a^-1，则a²等于（　　）

A．

B．

3$+\sqrt{5}$

C．

2$+\sqrt{3}$

D．

3$+\sqrt{13}$

分析根据立方和公式进行因式分解与化简，再利用完全平方公式，即可求出a²的值．

解答解：a³+a^-3=（a+a^-1）（a²-a•a^-1+a^-2）=a+a^-1，
所以a²-1+a^-2=1，
即a²-2+a^-2=0，
所以a⁴-2a²+1=0，
即（a²-1）²=0，
解得a²=1．
故选：A．

点评本题考查了立方和公式与完全平方公式的应用问题，是基础题目．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

12．在区间（0，1）内任取一个数a，能使方程x²+2ax+$\frac{1}{2}$=0有两个不相等的实数根的概率为（　　）

$\frac{2-\sqrt{2}}{2}$

9．已知函数y=3^x的图象经过点（-1，y₀），那么y₀等于（　　）

16．将函数y=-sin（$\frac{π}{3}$-x）的周期变为原来的2倍，再将新函数图象向右平移$\frac{π}{6}$个单位长度，得到y=f（x）的图象，则函数y=f（x）的解析式为y=sin（$\frac{1}{2}$x-$\frac{5π}{12}$）．

6．已知$\overrightarrow{a}$=（cosθ，-1），$\overrightarrow{b}$=（sinθ，2），当$\overrightarrow{a}$∥$\overrightarrow{b}$，求3cos²θ+2sin2θ

7．如图，在正方体ABCD-A₁B₁C₁D₁中．

（Ⅰ）如图（1）求CD₁与平面A₁B₁CD所成的角
（Ⅱ）如图（2）求证：A₁C∥平面AED₁．

4．

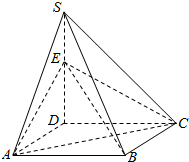如图，四棱锥S-ABCD的底面是正方形，SD⊥平面ABCD，SD=AD=a，点E是SD上的点，且DE=λa（0＜λ≤1）．
（Ⅰ）求证：对任意的λ∈（0，1），都有AC⊥BE；
（Ⅱ）若直线DE与平面ACE所成角大小为60°，求λ的值．

5．若函数y=log_ax（a＞0，且a≠1）的图象如图所示，则下列函数与其图象相符的是（　　）

试题分类