题目内容
13.一个四棱锥的底面为正方形,其三视图如图所示,则这个四棱锥的侧面积是3$\sqrt{2}$+$\sqrt{22}$.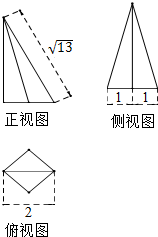
分析 此几何体为四棱锥P-ABCD,其底面为一个对角线长BD=2的正方形ABCD,由三视图知其中一个侧棱PD为棱锥的高,其相对的侧棱PB与高PD及底面正方形的对角线BD组成一个直角三角形,此侧棱长PB=$\sqrt{13}$,由此能求出这个四棱锥的侧面积.
解答 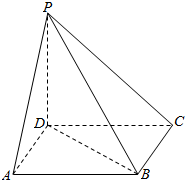 解:由题设及图知,此几何体为四棱锥P-ABCD,
解:由题设及图知,此几何体为四棱锥P-ABCD,
其底面为一个对角线长BD=2的正方形ABCD,
由三视图知其中一个侧棱PD为棱锥的高,其相对的侧棱PB与高PD及底面正方形的对角线BD组成一个直角三角形,
此侧棱长PB=$\sqrt{13}$,
故这个四棱锥的侧面积:
S=2S△PDC+2S△PBC
=2($\frac{1}{2}×PD×DC$+$\frac{1}{2}×BC×PC$)
=3$\sqrt{2}$+$\sqrt{22}$.
故答案为:$3\sqrt{2}+\sqrt{22}$.
点评 本题考查四棱锥的侧面积的求法,是中档题,解题时要认真审题,注意三视图的性质的合理运用.

练习册系列答案
相关题目
9.已知函数y=3x的图象经过点(-1,y0),那么y0等于( )
| A. | $\frac{1}{3}$ | B. | -$\frac{1}{3}$ | C. | 3 | D. | -3 |
1.在复平面内,复数z=(a-1)+(a+1)i(a∈R,i为虚数单位)对应的点位于第三象限的充要条件是( )
| A. | a>1 | B. | a<1 | C. | a>-1 | D. | a<-1 |
8.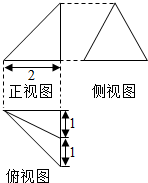 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
 某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )
某几何体的三视图如图所示,正视图为直角三角形,侧视图为等边三角形,俯视图为等腰直角三角形,则其外接球的表面积为( )| A. | 5π | B. | $\frac{20}{3}π$ | C. | 8π | D. | $\frac{28}{3}π$ |
18.某四棱锥的三视图如图所示,该四棱锥的体积是( )


| A. | 32 | B. | $\frac{32}{3}$ | C. | 48 | D. | $\frac{16}{3}$ |
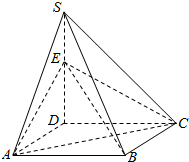 如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1).
如图,四棱锥S-ABCD的底面是正方形,SD⊥平面ABCD,SD=AD=a,点E是SD上的点,且DE=λa(0<λ≤1).



