题目内容
有一批金属零件，其中80%的重量不少于3公斤，现从这批零件中任取100个，试求其中至少有30个重量少于3公斤的概率．
考点：互斥事件的概率加法公式,相互独立事件的概率乘法公式
专题：概率与统计
分析：由题意，求出重量不少于3公斤的概率，再求出至少有30个重量大于3公斤的概率，根据概率的乘法公式计算即可．
解答：
解：现从这批零件中任取100个，重量不少于3公斤的有80个，重量不少于3公斤的概率有0.8，
至少有30个重量大于3公斤的概率为0.3，
则至少有30个重量少于3公斤的概率为0.3×0.8=0.24
至少有30个重量大于3公斤的概率为0.3，
则至少有30个重量少于3公斤的概率为0.3×0.8=0.24
点评：本题主要考查了互斥事件的概率的求法，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=-x2-x+2，则函数y=f（-x）的图象是（ ）
A、 |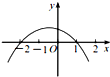
B、 |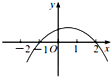
C、 |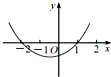
D、 |
已知A、B、C、D为同一球面上的四点，且连接每点间的线段长都等于2，则球心O到平面BCD的距离等于（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，在三棱锥A-BCD中，∠ABC=∠BCD=∠CDA=90°，设顶点A在底面BCD上的射影为E．