题目内容
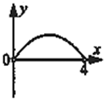
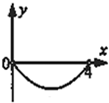
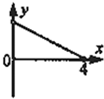
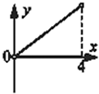
已知函数f（x）=x2sinx，则其在区间[-π，π]上的大致图象是（ ）
A、 |
B、 |
C、 |
D、 |
考点：函数的图象
专题：函数的性质及应用
分析：根据函数f（x）=x2sinx是奇函数，且函数在[0，π]上的函数值为正实数，从而得出结论．
解答：
解：由于函数f（x）=x2sinx是奇函数，
故它的图象关于原点对称，且当x∈[0，π]时，函数值为正实数，
故选D．
故它的图象关于原点对称，且当x∈[0，π]时，函数值为正实数，
故选D．
点评：本题主要考查奇函数的图象和性质，正弦函数在∈[0，π]上的值域，属于基础题．
练习册系列答案
相关题目
下列推理正确的是（ ）
| A、如果不买彩票，那么就不能中奖，因为你买了彩票，所以你一定中奖 | ||||||||||||||
| B、∵a＞b，a＞c，∴a-b＞a-c | ||||||||||||||
C、若a∈R+，ab＜0，则
| ||||||||||||||
D、若a，b∈R+，则lga+lgb≥2
|
根据给出的数塔猜测123456×9+7=（ ）
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…
| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |
在100件产品中有6件次品，现从中任取3件产品，至少有1件次品的不同取法的种数是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
如图，矩形纸片ABCD中，BC=4，AB=3，点P是BC边上的动点，现将△PCD沿PD翻折，得到△PFD；作∠BPF的角平分线交AB于点E．设BP=x，BE=y，则下列图象中，能表示y与x的函数关系的图象大致是（ ）
已知等比数列{an}中，a1a2a3a4a5=32，且a11=8，则a7的值为（ ）
| A、4 | ||
| B、-4 | ||
| C、±4 | ||
D、±2
|