题目内容
已知A、B、C、D为同一球面上的四点,且连接每点间的线段长都等于2,则球心O到平面BCD的距离等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:球内接多面体
专题:空间位置关系与距离
分析:设O为四面体ABCD外接球的球心,过A作AH⊥BCD于H,则O在AH上,延长BH交BC于E,连接OB、AE.可算出四面体的高AH=
,根据Rt△BOH∽Rt△AEH,得OH=
BO=
AO,所以OH=
AH=
,即球心到平面BCD的距离等于
.
2
| ||
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| ||
| 6 |
| ||
| 6 |
解答:
解:设O为四面体ABCD外接球的球心,过A作AH⊥BCD于H,则O在AH上
延长BH交BC于E,连接OB、AE
∵等边三角形BCD中,H为中心
∴BE⊥CD且E为CD的中点,可得BE=AE=
AB=
,
∴BH=
BE=
,
在Rt△ABH中,AH=
=
又∵Rt△BOH∽Rt△AEH
∴
=
,结合EH=
BE=
AE得:OH=
BO
∵AO=BO=R,(R是外接球半径)
∴OH=
AH=
,即球心到平面BCD的距离等于
故选:B

延长BH交BC于E,连接OB、AE
∵等边三角形BCD中,H为中心
∴BE⊥CD且E为CD的中点,可得BE=AE=
| ||
| 2 |
| 3 |
∴BH=
| 2 |
| 3 |
2
| ||
| 3 |
在Rt△ABH中,AH=
| AB2-BH2 |
2
| ||
| 3 |
又∵Rt△BOH∽Rt△AEH
∴
| OH |
| BO |
| EH |
| AE |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
∵AO=BO=R,(R是外接球半径)
∴OH=
| 1 |
| 4 |
| ||
| 6 |
| ||
| 6 |
故选:B
点评:本题给出正四面体的棱长,求它的外接球心到底面的距离,着重考查了正四面体的性质和多面体的外接球等知识点,属于基础题.

练习册系列答案
 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
在△ABC中,A,B,C是三角形的三内角,若sin(A-B)cosB+cos(A-B)sinB≥1,则该三角形是( )
| A、等腰三角形 | B、直角三角形 |
| C、正三角形 | D、不存在 |
根据给出的数塔猜测123456×9+7=( )
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…
1×9+2=11
12×9+3=111
123×9+4=1111
1234×9+5=11111
12345×9+6=111111
…
| A、1111110 |
| B、1111111 |
| C、1111112 |
| D、1111113 |
已知等比数列{an}中,a1a2a3a4a5=32,且a11=8,则a7的值为( )
| A、4 | ||
| B、-4 | ||
| C、±4 | ||
D、±2
|
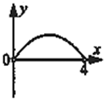
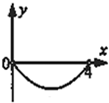
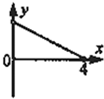
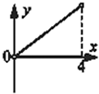
 如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点,现将△PCD沿PD翻折,得到△PFD;作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点,现将△PCD沿PD翻折,得到△PFD;作∠BPF的角平分线交AB于点E.设BP=x,BE=y,则下列图象中,能表示y与x的函数关系的图象大致是( )