题目内容
根据下列条件,求△ABC中的未知量.
(1)已知△ABC中,B=45°,C=75°,b=2,求a边长;
(2)已知b=4,c=8,B=30°,求a边.
(1)已知△ABC中,B=45°,C=75°,b=2,求a边长;
(2)已知b=4,c=8,B=30°,求a边.
考点:正弦定理
专题:解三角形
分析:(1)由条件利用三角形内角和公式求得A的值,再利用正弦定理求得a的值.
(2)由条件利用正弦定理求得sinC的值,可得C为直角,在理哦也难怪勾股定理求得a的值.
(2)由条件利用正弦定理求得sinC的值,可得C为直角,在理哦也难怪勾股定理求得a的值.
解答:
解:(1)∵已知△ABC中,B=45°,C=75°,b=2,由三角形内角和公式可得A=60°,
由正弦定理可得
=
,即
=
,求得a=
.
(2)已知△ABC中,∵已知b=4,c=8,B=30°,有正弦定理可得
=
,
即
=
,求得sinC=1,可得C=
,∴△ABC为直角三角形,
∴a=
=
=4
.
由正弦定理可得
| a |
| sinA |
| b |
| sinB |
| a | ||||
|
| 2 | ||||
|
| 6 |
(2)已知△ABC中,∵已知b=4,c=8,B=30°,有正弦定理可得
| b |
| sinB |
| c |
| sinC |
即
| 4 | ||
|
| 8 |
| sinC |
| π |
| 2 |
∴a=
| c2-b2 |
| 64-16 |
| 3 |
点评:本题主要考查三角形内角和公式、正弦定理的应用,属于基础题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
下列推理正确的是( )
| A、如果不买彩票,那么就不能中奖,因为你买了彩票,所以你一定中奖 | ||||||||||||||
| B、∵a>b,a>c,∴a-b>a-c | ||||||||||||||
C、若a∈R+,ab<0,则
| ||||||||||||||
D、若a,b∈R+,则lga+lgb≥2
|
已知等比数列{an}中,a1a2a3a4a5=32,且a11=8,则a7的值为( )
| A、4 | ||
| B、-4 | ||
| C、±4 | ||
D、±2
|
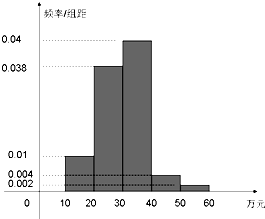 在某市的人大贿选案中,经调查统计该市人大代表的受贿情况的频率分布直方图如图:其中受贿[10,20]万元的有10人.
在某市的人大贿选案中,经调查统计该市人大代表的受贿情况的频率分布直方图如图:其中受贿[10,20]万元的有10人.