题目内容
椭圆
+
=1的焦点为F1，F2，
（1）P为椭圆上的一点，已知
•
=0，求△F1PF2的面积；
（2）动点P在椭圆的一动点，定点M（8，0），求PM中点Q轨迹方程．
| x2 |
| 25 |
| y2 |
| 9 |
（1）P为椭圆上的一点，已知
| PF1 |
| PF2 |
（2）动点P在椭圆的一动点，定点M（8，0），求PM中点Q轨迹方程．
考点：轨迹方程,平面向量数量积的运算
专题：向量与圆锥曲线,圆锥曲线的定义、性质与方程,坐标系和参数方程
分析：（1）根据向量数量积为0，求出
⊥
，进一步利用椭圆的定义求出三角形的面积．
（2）先把椭圆的标准方程转化成参数式，利用中点坐标求出关系，最后在转化成直角坐标的形式．
| PF1 |
| PF2 |
（2）先把椭圆的标准方程转化成参数式，利用中点坐标求出关系，最后在转化成直角坐标的形式．
解答：
解：（1）椭圆
+
=1的焦点为F1，F2，P为椭圆上的一点，已知
•
=0，
所以：
⊥
根据椭圆的定义：
+|
|=10
两边平方得：|
|2+|
|2+2|
||
|=100
解得：2|
||
|=36
S△PF1F2=
|
||
|=9
（2）椭圆
+
=1的参数方程为：
(θ为参数)
即P（5cosθ，3sinθ），M（8，0），
设Q（x，y）
则：
解得：
+
=1
所求的轨迹方程为：
+
=1
| x2 |
| 25 |
| y2 |
| 9 |
| PF1 |
| PF2 |
所以：
| PF1 |
| PF2 |
根据椭圆的定义：
| |PF1| |
| PF2 |
两边平方得：|
| PF1 |
| PF2 |
| PF |
| PF |
解得：2|
| PF |
| PF |
S△PF1F2=
| 1 |
| 2 |
| PF |
| PF |
（2）椭圆
| x2 |
| 25 |
| y2 |
| 9 |
|
即P（5cosθ，3sinθ），M（8，0），
设Q（x，y）
则：
|
解得：
| 4(x-4)2 |
| 25 |
| 4y2 |
| 9 |
所求的轨迹方程为：
| 4(x-4)2 |
| 25 |
| 4y2 |
| 9 |
点评：本题考查的知识要点：向量垂直的充要条件，三角形的面积，椭圆的定义，椭圆标准式与参数式得转化，中点坐标公式的应用．
练习册系列答案
相关题目
已知等比数列{an}满足a1+a2=10，a2+a3=15，则an=（ ）
A、4×(
| ||
B、4×(
| ||
C、4×(
| ||
D、4×(
|
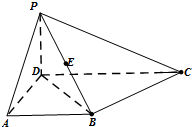如图，在四棱椎P-ABCD中，PD⊥平面ABCD，CD∥AB，CD⊥DA且PD=DA=AB=
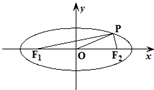如图，F1、F2是椭圆