Question

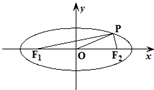如图，F₁、F₂是椭圆

x2

a2

+

y2

b2

=1的两个焦点，O为坐标原点，P是椭圆上的一点，且满足|F₁F₂|=2|OP|，若∠PF₂F₁=5∠PF₁F₂，则椭圆的离心率为（　　）

• A、

  3

  2

• B、

  6

  3

• C、

  2

  2

• D、

  2

  3

Answer 1

考点：椭圆的简单性质

专题：圆锥曲线的定义、性质与方程

分析：根据题意可知∠F₁PF₂=90°，∠PF₁F₂=5∠PF₂F₁，进而求得∠PF₁F₂和∠PF₂F₁，在Rt△PF₁F₂分别表示出|PF₁|和|PF₂|，进而根据椭圆的定义表示出a，进而求得a和c的关系，即椭圆的离心率．

解答： 解：∵|F₁F₂|=2|OP|，O是F₁F₂的中点，
∴∠F₁PF₂=90°
∵∠PF₁F₂=5∠PF₂F₁，
∴∠PF₁F₂=15°，∠PF₂F₁=75°
∴|PF₁|=|F₁F₂|sin∠PF₂F₁=2c•sin75°，∴|PF₂|=|F₁F₂|sin∠PF₁F₂=2c•sin15°，
∴2a=|PF₁|+|PF₂|=2c•sin75°+2c•sin15°=4csin45°cos30°=

6

c
∴a=

6

2

c
∴e=

c

a

=

6

3

故选B．

点评：本题主要考查了椭圆的简单性质．涉及了圆的性质，解三角形问题等．考查了学生综合分析问题的能力．