题目内容
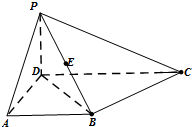 如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=
如图,在四棱椎P-ABCD中,PD⊥平面ABCD,CD∥AB,CD⊥DA且PD=DA=AB=| 1 |
| 2 |
(1)证明:平面PBD⊥平面PBC;
(2)求AB与平面PBC所成角的正弦值;
(3)求钝二面角A-PB-C的大小.
考点:二面角的平面角及求法,平面与平面垂直的判定,直线与平面所成的角
专题:空间位置关系与距离,空间角,空间向量及应用
分析:(1)根据条件可分别以DA,DC,DP三条直线为x轴,y轴,z轴建立空间直角坐标系,根据已知的边的长度求出点A,B,C,D,P点的坐标,要证明两平面垂直,根据面面垂直的判定定理,只要一个平面内一条直线和另一个平面垂直即可.已知PD⊥平面ABCD,所以得到PD⊥BC,所以试着看BC能否垂直BD,若和BD垂直,便可得到BC⊥平面PBD,这时候可以求出向量
,
的坐标,然后求
•
=0,所以BC⊥BD,这样该问就得到了证明;
(2)要求AB与平面PBC所成角的正弦值,可求
与平面PBC法向量夹角余弦值的绝对值,所以设
=(x1,y1,z1),根据
⊥
,
⊥
,然后得到对应数量积为0即可求出
,
的坐标可求出来,所以便可根据两向量夹角的余弦公式求出
,
夹角余弦值的绝对值;
(3)要求钝二面角A-PB-C的大小,可求平面PAB和平面PBC法向量夹角,根据法向量夹角和二面角的大小相等或互补的特点即可求出该钝二面角的大小,可设平面PAB的法向量为
,根据(2)中求
的方法求出
,然后求出cos<
,
>,从而求出<
,
>,继而求得该钝二面角的大小.
| DB |
| BC |
| DB |
| BC |
(2)要求AB与平面PBC所成角的正弦值,可求
| AB |
| n1 |
| n1 |
| BC |
| n1 |
| BP |
| n1 |
| AB |
| n1 |
| AB |
(3)要求钝二面角A-PB-C的大小,可求平面PAB和平面PBC法向量夹角,根据法向量夹角和二面角的大小相等或互补的特点即可求出该钝二面角的大小,可设平面PAB的法向量为
| n2 |
| n1 |
| n2 |
| n1 |
| n2 |
| n1 |
| n2 |
解答:
解:(1)根据已知条件知,DA,DC,DP三条直线两两垂直,所以分别以这三条直线为x轴,y轴,z轴建立如图所示空间直角坐标系:
 根据已知的边的长度可求以下几点坐标:
根据已知的边的长度可求以下几点坐标:
D(0,0,0),A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1);
∴
=(1,1,0),
=(-1,1,0);
∴
•
=0,∴
⊥
,即BC⊥DB,又PD⊥平面ABCD,BC?平面ABCD;
∴PD⊥BC,即BC⊥PD,PD∩DB=D;
∴BC⊥平面PBD,BC?平面PBC;
∴平面PBC⊥平面PBD,即平面PBD⊥平面PBC;
(2)设平面PBC的法向量为
=(x1,y1,z1),
=(-1,-1,1)则:
,∴
;
∴
,取z1=2,则
=(1,1,2),
=(0,1,0);
∴AB与平面PBC所成角的正弦值等于
与
所夹角的余弦值的绝对值;
|cos<
,
>|=|
|=
=
;
∴AB与平面PBC所成角的正弦值为
;
(3)设平面PAB的法向量为
=(x2,y2,z2),根据(2)求
的方法同理可求得
=(1,0,1);
∴cos<
,
>=
=
=
;
∴<
,
>=30°;
∴钝二面角A-PB-C的大小为150°.
 根据已知的边的长度可求以下几点坐标:
根据已知的边的长度可求以下几点坐标:D(0,0,0),A(1,0,0),B(1,1,0),C(0,2,0),P(0,0,1);
∴
| DB |
| BC |
∴
| DB |
| BC |
| DB |
| BC |
∴PD⊥BC,即BC⊥PD,PD∩DB=D;
∴BC⊥平面PBD,BC?平面PBC;
∴平面PBC⊥平面PBD,即平面PBD⊥平面PBC;
(2)设平面PBC的法向量为
| n1 |
| BP |
|
|
∴
|
| n1 |
| AB |
∴AB与平面PBC所成角的正弦值等于
| AB |
| n1 |
|cos<
| AB |
| n1 |
| ||||
|
|
| 1 | ||
|
| ||
| 6 |
∴AB与平面PBC所成角的正弦值为
| ||
| 6 |
(3)设平面PAB的法向量为
| n2 |
| n1 |
| n2 |
∴cos<
| n1 |
| n2 |
| ||||
|
|
| 3 | ||||
|
| ||
| 2 |
∴<
| n1 |
| n2 |
∴钝二面角A-PB-C的大小为150°.
点评:考查建立空间直角坐标系,利用空间向量证明直线的垂直,求直线和平面所成角,以及二面角的大小的方法,线面垂直的判定定理,面面垂直的判定定理,以及向量数量积的坐标运算,向量夹角的余弦公式,二面角的概念.

练习册系列答案
相关题目
若集合A={x|y=
},B={y|y=ex(x≥0},则A∩B等于( )
| 1-x |
| A、[1,+∞) | B、(0,1] |
| C、R | D、{1} |