题目内容
若对于给定的正实数k,函数f(x)=
的图象上总存在点C,使得以C为圆心,1为半径的圆上有两个不同的点到原点O的距离为2,则k的取值范围是 .
| k |
| x |
考点:圆方程的综合应用
专题:综合题,直线与圆
分析:根据题意得:以C为圆心,1为半径的圆与原点为圆心,2为半径的圆有两个交点,即C到原点距离小于3,即f(x)的图象上离原点最近的点到原点的距离小于3,设出C坐标,利用两点间的距离公式表示出C到原点的距离,利用基本不等式求出距离的最小值,让最小值小于3列出关于k的不等式,求出不等式的解集即可得到k的范围.
解答:
解:根据题意得:|OC|<1+2=3,
设C(x,
),
∵|OC|=
≥
,
∴
<3,即0<k<
,
则k的范围为(0,
).
故答案为:(0,
).
设C(x,
| k |
| x |
∵|OC|=
x2+
|
| 2k |
∴
| 2k |
| 9 |
| 2 |
则k的范围为(0,
| 9 |
| 2 |
故答案为:(0,
| 9 |
| 2 |
点评:此题考查了直线与圆的位置关系,涉及的知识有:圆与圆位置关系的判定,基本不等式的运用,以及两点间的距离公式,解题的关键是根据题意得出以C为圆心,1为半径的圆与原点为圆心,2为半径的圆有两个交点,即C到原点距离小于3.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
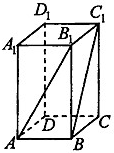 如图,在长方体ABCD-A1B1C1D1中,AB=
如图,在长方体ABCD-A1B1C1D1中,AB=| 2 |
| 3 |
| 6 |
| A、60° | B、45° |
| C、30° | D、15° |
设二次函数f(x)=-x2+x+a(a<0),若f(m)>0,则f(m+1)的值为( )
| A、正数 | B、负数 |
| C、非负数 | D、正数、负数或零都有可能 |
若直线l1:(2a+3)x+(a-1)y+3=0与l2:(a+2)x+(1-a)y-3=0平行,则实数a的值为( )
| A、l | ||
B、-
| ||
C、1或-
| ||
| D、1或-l |