Question

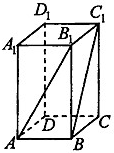如图，在长方体ABCD-A₁B₁C₁D₁中，AB=

2

，BC=

3

，AA₁=

6

，则异面直线AB₁与BC₁所成角的大小为（　　）

• A、60°
• B、45°
• C、30°
• D、15°

Answer 1

考点：异面直线及其所成的角

专题：计算题,作图题,空间位置关系与距离

分析：连结AD₁，B₁D₁，化异面直线AB₁与BC₁所成角为∠B₁AD₁，用余弦定理解答．

解答： 解：如图：
连结AD₁，B₁D₁，
则异面直线AB₁与BC₁所成角为∠B₁AD₁，
在△B₁AD₁中，
AB₁=

2+6

=2

2

；AD₁=

3+6

=3；B₁D₁=

2+3

=

5

；
则cos∠B₁AD₁=

9+8-5

2×3×2 2

=

2

2

，
∴∠B₁AD₁=45°，
故选B．

点评：本题考查了学生的空间想象力及辅助线的作法，同时考查了余弦定理的应用，属于基础题．