题目内容
已知函数f(x)=x3+3mx2+nx+m2.在x=-1处有极值0;
(Ⅰ)求m,n的值;
(Ⅱ)求f(x)的单调区间.
(Ⅰ)求m,n的值;
(Ⅱ)求f(x)的单调区间.
考点:利用导数研究函数的单调性,利用导数研究函数的极值
专题:导数的概念及应用
分析:(Ⅰ)先求出f′(x)=3x2+6mx+n,得方程组
,解出即可;
(Ⅱ)由(Ⅰ)得:①当m=1,n=3时f′(x)=3(x+1)2≥0恒成立,即x=-1不是f(x)的极值点,舍去.②当m=2,n=9时f′(x)=3(x+1)(x+3),所以f(x)在x=-1处有极值,故m=2,n=9;∴f(x)的减区间是(-3,-1);增区间是(-∞,-3),(-1,+∞).
|
(Ⅱ)由(Ⅰ)得:①当m=1,n=3时f′(x)=3(x+1)2≥0恒成立,即x=-1不是f(x)的极值点,舍去.②当m=2,n=9时f′(x)=3(x+1)(x+3),所以f(x)在x=-1处有极值,故m=2,n=9;∴f(x)的减区间是(-3,-1);增区间是(-∞,-3),(-1,+∞).
解答:
解:(Ⅰ)∵f′(x)=3x2+6mx+n
∴
,
解得:
,或
,
(Ⅱ)由(Ⅰ)得:
①当m=1,n=3时f′(x)=3(x+1)2≥0恒成立,
即x=-1不是f(x)的极值点,舍去.
②当m=2,n=9时f′(x)=3(x+1)(x+3),
当-3<x<-1时,f’(x)<0,f(x)单调递减,
当x>-1 或 x<-3 时,f’(x)>0,f(x)单调递增,
所以f(x)在x=-1处有极值,故m=2,n=9;
∴f(x)的减区间是(-3,-1);增区间是(-∞,-3),(-1,+∞).
∴
|
解得:
|
|
(Ⅱ)由(Ⅰ)得:
①当m=1,n=3时f′(x)=3(x+1)2≥0恒成立,
即x=-1不是f(x)的极值点,舍去.
②当m=2,n=9时f′(x)=3(x+1)(x+3),
当-3<x<-1时,f’(x)<0,f(x)单调递减,
当x>-1 或 x<-3 时,f’(x)>0,f(x)单调递增,
所以f(x)在x=-1处有极值,故m=2,n=9;
∴f(x)的减区间是(-3,-1);增区间是(-∞,-3),(-1,+∞).
点评:本题考察了函数的单调性,求函数的极值问题,导数的应用,是一道基础题.

练习册系列答案
相关题目
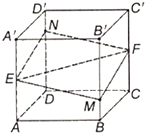 如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下五个命题:
如图所示,正方体ABCD-A′B′C′D′的棱长为1,E,F分别是棱AA′,CC′的中点,过直线E,F的平面分别与棱BB′、DD′交于M,N,设BM=x,x∈[0,1],给出以下五个命题: