题目内容
已知f(x)=-
ax2+(1-a)x+lnx.
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当a=0时,令g(x)=f(x)-x,求经过点(-e,-1)且与曲线g(x)相切的直线方程.
| 1 |
| 2 |
(Ⅰ)讨论函数f(x)的单调性;
(Ⅱ)当a=0时,令g(x)=f(x)-x,求经过点(-e,-1)且与曲线g(x)相切的直线方程.
考点:利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)求函数的导数,讨论a的取值范围,即可判断函数f(x)的单调性;
(Ⅱ)当a=0时,求出g(x)=f(x)-x,设出切点坐标求出对应的切线方程即可得到结论.
(Ⅱ)当a=0时,求出g(x)=f(x)-x,设出切点坐标求出对应的切线方程即可得到结论.
解答:
解:(Ⅰ)函数的定义域为(0,+∞),
函数的导数为f′(x)=-ax+1-a+
=
,(x>0),
若a≤0,则1-ax>0,则此时f′(x)>0,函数单调递增,即此时函数的增区间为(0,+∞),
当a>0.此时
>0,此时只需要考虑1-ax的符号,
当f′(x)>0,解得0<x<
,此时函数单调递增,
当f′(x)<0,解得x>
,此时函数单调递减,
综上a≤0,f(x)在(0,+∞)上递增,a>0时,函数的增区间为(0,
),减区间为(
,+∞).
(Ⅱ)当a=0时,令g(x)=f(x)-x=lnx,
设切点坐标为(n,lnn),则k=f′(n)=
,
此时切线方程为y-lnn=
(x-n),
∵切线过点(-e,-1),
则-1-lnn=
(-e-n),
即nlnn=e,解得n=e,
下证明根的唯一性,
当0<n<e时,nlnn<nlne<n<e,
当n>e时,nlnn>nlne>n>e,
则方程nlnn=e只有唯一的根n=e.
函数的导数为f′(x)=-ax+1-a+
| 1 |
| x |
| (1-ax)(x+1) |
| x |
若a≤0,则1-ax>0,则此时f′(x)>0,函数单调递增,即此时函数的增区间为(0,+∞),
当a>0.此时
| 1+x |
| x |
当f′(x)>0,解得0<x<
| 1 |
| a |
当f′(x)<0,解得x>
| 1 |
| a |
综上a≤0,f(x)在(0,+∞)上递增,a>0时,函数的增区间为(0,
| 1 |
| a |
| 1 |
| a |
(Ⅱ)当a=0时,令g(x)=f(x)-x=lnx,
设切点坐标为(n,lnn),则k=f′(n)=
| 1 |
| n |
此时切线方程为y-lnn=
| 1 |
| n |
∵切线过点(-e,-1),
则-1-lnn=
| 1 |
| n |
即nlnn=e,解得n=e,
下证明根的唯一性,
当0<n<e时,nlnn<nlne<n<e,
当n>e时,nlnn>nlne>n>e,
则方程nlnn=e只有唯一的根n=e.
点评:本题主要考查函数单调性的判断,以及利用导数的几何意义求切线方程,综合考查导数的性质.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
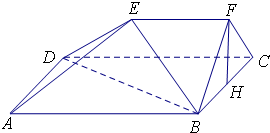 如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=
如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=