题目内容
已知数列{an}的前n项和为Sn,a1=1,an+1=2Sn+1(n∈N*),等差数列{bn}中,公差d=2,且b1+b2+b3=15.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)求数列{an•bn}的前n项和Tn.
(Ⅰ)求数列{an}、{bn}的通项公式;
(Ⅱ)求数列{an•bn}的前n项和Tn.
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)an+1=2Sn+1⇒an=2Sn-1+1(n≥2,n∈N*),两式相减,可得an+1=3an(n∈N*),从而可得数列{an}的通项公式;由等差数列{bn}中,公差d=2,且b1+b2+b3=15可求得{bn}的通项公式;
(Ⅱ)由(Ⅰ)知an•bn=(2n+1)×3n-1,利用错位相减法即可求得数列{an•bn}的前n项和Tn.
(Ⅱ)由(Ⅰ)知an•bn=(2n+1)×3n-1,利用错位相减法即可求得数列{an•bn}的前n项和Tn.
解答:
解:(Ⅰ))∵an+1=2Sn+1(n≥1,n∈N*),∴an=2Sn-1+1(n≥2,n∈N*),
∴an+1-an=2an,即an+1=3an(n≥2,n∈N*),…2分
又a1=1,a2=2a1+1=3,
∴a2=3a1,∴an+1=3an(n∈N*).
∵a1=1,∴数列{an}是首项为1,公比为3的等比数列,
∴an=3n-1(n∈N*)…4分
∵b1+b2+b3=15,∴b2=5,又d=2,∴b1=b2-d=3,…6分
∴bn=3+2(n-1)=2n+1…7分
(Ⅱ)由(Ⅰ)知,Tn=3×1+5×3+7×32+…+(2n-1)×3n-2+(2n+1)×3n-1,①
3Tn=3×3+5×32+7×33+…+(2n-1)×3n-1+(2n+1)×3n,②
∴①-②得:-2Tn=3×1+2×3+2×32+…+2×3n-1-(2n+1)×3n
=3+2(3+32+33+…+3n-1)-(2n+1)×3n
=3+2×
-(2n+1)×3n…10分
=-2n•3n…11分
∴Tn=n•3n(n∈N*)…12分
∴an+1-an=2an,即an+1=3an(n≥2,n∈N*),…2分
又a1=1,a2=2a1+1=3,
∴a2=3a1,∴an+1=3an(n∈N*).
∵a1=1,∴数列{an}是首项为1,公比为3的等比数列,
∴an=3n-1(n∈N*)…4分
∵b1+b2+b3=15,∴b2=5,又d=2,∴b1=b2-d=3,…6分
∴bn=3+2(n-1)=2n+1…7分
(Ⅱ)由(Ⅰ)知,Tn=3×1+5×3+7×32+…+(2n-1)×3n-2+(2n+1)×3n-1,①
3Tn=3×3+5×32+7×33+…+(2n-1)×3n-1+(2n+1)×3n,②
∴①-②得:-2Tn=3×1+2×3+2×32+…+2×3n-1-(2n+1)×3n
=3+2(3+32+33+…+3n-1)-(2n+1)×3n
=3+2×
| 3(1-3n-1) |
| 1-3 |
=-2n•3n…11分
∴Tn=n•3n(n∈N*)…12分
点评:本题考查等比数列关系的确定与等差数列通项公式的应用,突出考查错位相减法求和,考查综合运算与求解能力,属于难题.

练习册系列答案
相关题目
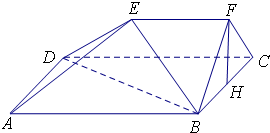 如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE=
如图,在五面体ABCDEF中,四边形ABCD是边长为2的正方形,EF∥平面ABCD,EF=1,FB=FC,∠BFC=90°,AE= 如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD.
如图所示,在四棱锥P-ABCD中,底面ABCD为正方形,PA⊥平面ABCD.