题目内容
2.在△ABC中,∠A=90°,AB=2,AC=4,E,F分别为AB,BC的中点,则$\overrightarrow{CE}•\overrightarrow{AF}$=-6.分析 根据题意画出图形,结合图形,利用平面向量的线性表示与数量积运算性质,即可求出$\overrightarrow{CE}•\overrightarrow{AF}$的值.
解答 解:如图所示,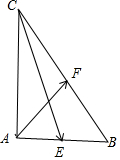
△ABC中,∠A=90°,AB=2,AC=4,E,F分别为AB,BC的中点,
则$\overrightarrow{CE}•\overrightarrow{AF}$=($\overrightarrow{CA}$+$\overrightarrow{AE}$)•$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AB}$)
=(-$\overrightarrow{AC}$+$\frac{1}{2}$$\overrightarrow{AB}$)•$\frac{1}{2}$($\overrightarrow{AC}$+$\overrightarrow{AB}$)
=-$\frac{1}{2}$${\overrightarrow{AC}}^{2}$-$\frac{1}{4}$$\overrightarrow{AC}$•$\overrightarrow{AB}$+$\frac{1}{4}$${\overrightarrow{AB}}^{2}$
=-$\frac{1}{2}$×42-$\frac{1}{4}$×0+$\frac{1}{4}$×22
=-6.
故答案为:-6.
点评 本题考查平面向量的线性表示与数量积运算问题,是基础题目.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
12.已知集合A={x|2<x<4},B={x|x<3或x>5},则A∪∁RB=( )
| A. | {x|2<x≤5} | B. | {x|x<4或x>5} | C. | {x|2<x<3} | D. | {x|x<2或x≥5} |
13.过点(-3,-1)且与直线x-2y+3=0平行的直线方程是( )
| A. | 2x+y+7=0 | B. | 2x-y+5=0 | C. | x-2y+1=0 | D. | x-2y+5=0 |
10.已知△ABC的外接圆半径为2,D为该圆上一点,且$\overrightarrow{AB}$+$\overrightarrow{AC}$=$\overrightarrow{AD}$,则△ABC的面积的最大值为( )
| A. | 3 | B. | 4 | C. | 3$\sqrt{3}$ | D. | 4$\sqrt{3}$ |
 如图所示,在三棱柱ABC-A1B1C1中,四边形AA1B1B为边长为2的正方形,四边形BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C,点E、F分别是B1C,AA1的中点.
如图所示,在三棱柱ABC-A1B1C1中,四边形AA1B1B为边长为2的正方形,四边形BB1C1C为菱形,∠BB1C1=60°,平面AA1B1B⊥平面BB1C1C,点E、F分别是B1C,AA1的中点.