题目内容
17.已知数列{an}满足:a1=2,an+1=$\left\{\begin{array}{l}{\frac{1}{2}{a}_{n},n为偶数}\\{{a}_{n}+1,n为奇数}\end{array}\right.$,若bn=a2n-1-1.(Ⅰ)求证:数列{bn}是等比数列;
(Ⅱ)若数列{an}的前n项和为Sn,求S2n.
分析 (Ⅰ)利用递推关系、等比数列的定义即可得出.
(Ⅱ)利用分组求和、等比数列的求和公式即可得出.
解答 解:(Ⅰ)证明:${b_{n+1}}={a_{2n+1}}-1=\frac{1}{2}{a_{2n}}-1$=$\frac{1}{2}({a_{2n-1}}+1)-1$=$\frac{1}{2}({a_{2n-1}}-1)=\frac{1}{2}{b_n}$,
故{bn} 为等比数列;
(Ⅱ)由(Ⅰ)知${b_n}=({a_1}-1)•{(\frac{1}{2})^{n-1}}=\frac{1}{{{2^{n-1}}}}$,∴${a_{2n-1}}=\frac{1}{{{2^{n-1}}}}+1$,
又a2n=a2n-1+1,∴${a_{2n-1}}+{a_{2n}}=\frac{1}{{{2^{n-2}}}}+3$,
∴${S_{2n}}=3n+\frac{{2(1-\frac{1}{2^n})}}{{1-\frac{1}{2}}}=3n+4-\frac{1}{{{2^{n-2}}}}$.
点评 本题考查了递推关系、等比数列的定义与求和公式、分组求和,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知直线l过点P(2,4),且与圆O:x2+y2=4相切,则直线l的方程为( )
| A. | x=2或3x-4y+10=0 | B. | x=2或x+2y-10=0 | C. | y=4或3x-4y+10=0 | D. | y=4或x+2y-10=0 |
5.命题p:甲的数学成绩不低于100分,命题q:乙的数字成绩低于100分,则p∨(¬q)表示( )
| A. | 甲、乙两人数学成绩都低于100分 | |
| B. | 甲、乙两人至少有一人数学成绩低于100分 | |
| C. | 甲、乙两人数学成绩都不低于100分 | |
| D. | 甲、乙两人至少有一人数学成绩不低于100分 |
12.设a,b,c∈R且c≠0.
若上表中的对数值恰有两个是错误的,则a的值为( )
| x | 1.5 | 3 | 5 | 6 | 7 | 8 | 9 | 14 | 27 |
| lgx | 2a+b | a+b | a-c+1 | b+c | a+2b+c | 3(c-a) | 2(a+b) | b-a | 3(a+b) |
| A. | lg$\frac{2}{21}$ | B. | $\frac{1}{2}$lg$\frac{3}{14}$ | C. | $\frac{1}{2}$lg$\frac{3}{7}$ | D. | lg$\frac{6}{7}$ |
6.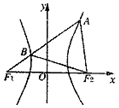 如图,F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1(b>0)$的左、右焦点,过F1的直线l与双曲线分别交于点A、B,若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1(b>0)$的左、右焦点,过F1的直线l与双曲线分别交于点A、B,若△ABF2为等边三角形,则△BF1F2的面积为( )
 如图,F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1(b>0)$的左、右焦点,过F1的直线l与双曲线分别交于点A、B,若△ABF2为等边三角形,则△BF1F2的面积为( )
如图,F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1(b>0)$的左、右焦点,过F1的直线l与双曲线分别交于点A、B,若△ABF2为等边三角形,则△BF1F2的面积为( )| A. | $8\sqrt{3}$ | B. | $9\sqrt{3}$ | C. | $18\sqrt{3}$ | D. | $27\sqrt{3}$ |
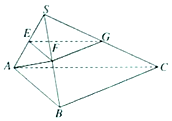 如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证:
如图,在三棱锥S-ABC中,平面SAB⊥平面SBC,AB⊥BC,AS=AB,点E、F、G分别是棱SA、SB、SC的中点.求证: