题目内容
14．已知x与y之间的一组数据：| x | 3 | 4 | 5 | 5 | 7 |
| y | 2 | 4 | 5 | 6 | 8 |
| A． | （5，5） | B． | （4.5，5） | C． | （4.8，5） | D． | （5，6） |
分析 要求y与x的线性回归方程为y=bx+a必过的点，需要先求出这组数据的样本中心点，根据所给的表格中的数据，求出横标和纵标的平均值，得到样本中心点，得到结果．
解答 解：由$\overline{x}$=$\frac{1}{5}$（3+4+5+5+7）=4.8，
$\overline{y}$=$\frac{1}{5}$（2+4+5+6+8）=5，
故线性回归方程过（4.8，5），
故选：C．
点评 本题考查线性回归方程必过样本中心点，这是一个基础题，题目的运算量不大，本题是一个只要认真就能够得分的题目．
练习册系列答案
相关题目
4．已知函数f（x）=（x2+ax+b）（ex-e），a，b∈R，当x＞0时，f（x）≥0，则实数a的取值范围为（ ）
| A． | -2≤a≤0 | B． | -1≤a≤0 | C． | a≥-1 | D． | 0≤a≤1 |
5．命题p：甲的数学成绩不低于100分，命题q：乙的数字成绩低于100分，则p∨（￢q）表示（ ）
| A． | 甲、乙两人数学成绩都低于100分 | |
| B． | 甲、乙两人至少有一人数学成绩低于100分 | |
| C． | 甲、乙两人数学成绩都不低于100分 | |
| D． | 甲、乙两人至少有一人数学成绩不低于100分 |
19．在中学生综合素质评价某个维度的测评中，分“优秀、合格、尚待改进”三个等级进行学生互评．某校高一年级有男生500人，女生400人，为了了解性别对该维度测评结果的影响，采用分层抽样方法从高一年级抽取了45名学生的测评结果，并作出频数统计表如下：
表1：男生
表2：女生
（1）求出表中的x，y
（2）从表二的非优秀学生中随机选取2人交谈，求所选2人中恰有1人测评等级为合格的概率．
表1：男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
（2）从表二的非优秀学生中随机选取2人交谈，求所选2人中恰有1人测评等级为合格的概率．
6．
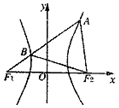如图，F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1（b＞0）$的左、右焦点，过F1的直线l与双曲线分别交于点A、B，若△ABF2为等边三角形，则△BF1F2的面积为（ ）
如图，F1、F2是双曲线$\frac{x^2}{9}-\frac{y^2}{b^2}=1（b＞0）$的左、右焦点，过F1的直线l与双曲线分别交于点A、B，若△ABF2为等边三角形，则△BF1F2的面积为（ ）| A． | $8\sqrt{3}$ | B． | $9\sqrt{3}$ | C． | $18\sqrt{3}$ | D． | $27\sqrt{3}$ |
