题目内容
17.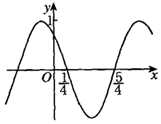 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )| A. | ω=π | |
| B. | φ=$\frac{π}{4}$ | |
| C. | f(x)的单调减区间为(2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z | |
| D. | f(x)的对称中心是(k+$\frac{1}{4}$,0),k∈Z |
分析 由题意和图象求出函数的周期,由周期公式求出ω的值,可判断出A;把点($\frac{1}{4}$,0)代入解析式化简后,由题意求出φ的值判断出B;由整体思想和正弦函数的单调性求出递减区间,判断出C;由整体思想和正弦函数的对称中心求出f(x)的对称中心,判断出D.
解答 解:由图象得,A=1,$\frac{1}{2}$T=$\frac{5}{4}-\frac{1}{4}$=1,则T=2,
由$T=\frac{2π}{ω}=2$ 得,ω=π,则A正确;
因为过点($\frac{1}{4}$,0),所以sin($\frac{1}{4}$π+φ)=0,
则$\frac{1}{4}$π+φ=kπ(k∈Z),φ=$-\frac{π}{4}$+kπ(k∈Z),
又|φ|<π,则φ=$-\frac{π}{4}$或$\frac{3π}{4}$,所以f(x)=sin(πx$-\frac{π}{4}$)或f(x)=sin(πx+$\frac{3π}{4}$),则B错误;
当f(x)=sin(πx+$\frac{3π}{4}$)时,
由$\frac{π}{2}+2kπ≤πx+\frac{3π}{4}≤\frac{3π}{2}+2kπ(k∈Z)$得,$-\frac{1}{4}+2k≤x≤\frac{3π}{4}+2k(k∈Z)$,
所以函数的递减区间是(2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z,则C正确;
当f(x)=sin(πx$-\frac{π}{4}$)时,由πx$-\frac{π}{4}$=kπ(k∈Z)得,x=k+$\frac{1}{4}$(k∈Z),
所以f(x)的对称中心是(k+$\frac{1}{4}$,0),k∈Z,则D正确;
故选B.
点评 本题考查由图象求形如y=Asin(ωx+φ)的解析式,正弦函数的单调性、对称中心,以及整体思想,属于中档题.

 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
甲图书馆
| 借书等待时间T1(分钟) | 1 | 2 | 3 | 4 | 5 |
| 频数 | 1500 | 1000 | 500 | 500 | 1500 |
| 借书等待时间T2(分钟) | 1 | 2 | 3 | 4 | 5 |
| 频数 | 1000 | 500 | 2000 | 1250 | 250 |
(2)以表中等待时间的学生人数的频率为概率,若某同学希望借书等待时间不超过3分钟,请问在哪个图书馆借更能满足他的要求?
| A. | (-∞,-1] | B. | (-∞,$\sqrt{2}$] | C. | [-1,$\sqrt{2}$] | D. | [$\sqrt{2}$,+∞) |
| A. | $\frac{7}{5}$ | B. | -$\frac{7}{5}$ | C. | $\frac{1}{5}$ | D. | -$\frac{1}{5}$ |
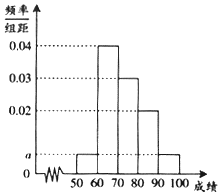 某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x::y | 1:1 | 2:1 | 3:4 | 4:5 |
(2)根据频率分布直方图,估计这100名学生语文成绩的中位数;
(3)若这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比如下表所示,求数学成绩在[50,90)之外的人数.(分数可以不为整数)