题目内容
9．已知α为第二象限角．且sin2α=-$\frac{24}{25}$，则cosα-sinα的值为（ ）| A． | $\frac{7}{5}$ | B． | -$\frac{7}{5}$ | C． | $\frac{1}{5}$ | D． | -$\frac{1}{5}$ |
分析 由α的范围和三角函数值的符号判断出cosα-sinα的符号，由条件、平方关系、二倍角的正弦函数求出cosα-sinα的值．
解答 解：∵α为第二象限角，∴cosα-sinα＜0，
∵sin2α=-$\frac{24}{25}$，
∴cosα-sinα=-$\sqrt{（cosα-sinα）^{2}}$=$-\sqrt{1-sin2α}$
=$-\sqrt{1+\frac{24}{25}}$=$-\frac{7}{5}$，
故选B．
点评 本题考查二倍角的正弦函数，平方关系，以及三角函数值的符号，属于基础题．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
17．
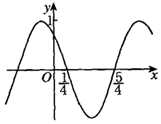已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则下列说法错误的是（ ）
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜π）的部分图象如图所示，则下列说法错误的是（ ）| A． | ω=π | |
| B． | φ=$\frac{π}{4}$ | |
| C． | f（x）的单调减区间为（2k-$\frac{1}{4}$，2k+$\frac{3}{4}$），k∈Z | |
| D． | f（x）的对称中心是（k+$\frac{1}{4}$，0），k∈Z |
14．
传承传统文化再掀热潮，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏．将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级，随机从中抽取了100名选手进行调查，下面是根据调查结果绘制的选手等级人数的条形图．
（Ⅰ）若将一般等级和良好等级合称为合格等级，根据已知条件完成下面的2×2列联表，并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关？
注：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
（Ⅱ）若参赛选手共6万人，用频率估计概率，试估计其中优秀等级的选手人数；
（Ⅲ）在优秀等级的选手中取6名，依次编号为1，2，3，4，5，6，在良好等级的选手中取6名，依次编号为1，2，3，4，5，6，在选出的6名优秀等级的选手中任取一名，记其编号为a，在选出的6名良好等级的选手中任取一名，记其编号为b，求使得方程组$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$有唯一一组实数解（x，y）的概率．
传承传统文化再掀热潮，央视科教频道以诗词知识竞赛为主的《中国诗词大会》火爆荧屏．将中学组和大学组的参赛选手按成绩分为优秀、良好、一般三个等级，随机从中抽取了100名选手进行调查，下面是根据调查结果绘制的选手等级人数的条形图．（Ⅰ）若将一般等级和良好等级合称为合格等级，根据已知条件完成下面的2×2列联表，并据此资料你是否有95%的把握认为选手成绩“优秀”与文化程度有关？
| 优秀 | 合格 | 合计 | |
| 大学组 | |||
| 中学组 | |||
| 合计 |
| P（k2≥k0） | 0.10 | 0.05 | 0.005 |
| k0 | 2.706 | 3.841 | 7.879 |
（Ⅲ）在优秀等级的选手中取6名，依次编号为1，2，3，4，5，6，在良好等级的选手中取6名，依次编号为1，2，3，4，5，6，在选出的6名优秀等级的选手中任取一名，记其编号为a，在选出的6名良好等级的选手中任取一名，记其编号为b，求使得方程组$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$有唯一一组实数解（x，y）的概率．
4．已知等差数列{an}中，公差d≠0，a4=10，且a3，a6，a10成等比数列，则数列{an}前9项的和为（ ）
| A． | 99 | B． | 90 | C． | 84 | D． | 70 |
1．若无论实数a取何值时，直线ax+y+a+1=0与圆x2+y2-2x-2y+b=0都相交，则实数b的取值范围．（ ）
| A． | （-∞，2） | B． | （2，+∞） | C． | （-∞，-6） | D． | （-6，+∞） |
18．已知平面向量$\overrightarrow a，\overrightarrow b$满足$\overrightarrow b•（\overrightarrow a+\overrightarrow b）=3$，且$|\overrightarrow a|=1，|\overrightarrow b|=2$，则向量$\overrightarrow a$与$\overrightarrow b$的夹角（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |