��Ŀ����
5����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0������P��2��1������������Ϊ$\frac{\sqrt{3}}{2}$����������Բ�ķ��̣�
������OΪ����ԭ�㣬����Բ������������M��N����$\overrightarrow{OM}$=$\overrightarrow{NO}$��ֱ��PM��PN�ֱ���Բ��A��B��
��i����֤��ֱ��AB�����㣬�������������ꣻ
��ii�����OAB��������ֵ��
���� �����������ʹ�ʽ����P������Բ���̣��������a��b��ֵ�������Բ���̣�
����i����ֱ��AB�ķ���Ϊy=kx+t��������Բ���̣�����ֱ�ߵĵ�бʽ���̣����M��N�����꣬��$\overrightarrow{OM}$=$\overrightarrow{NO}$������Τ�ﶨ��������t=-2ʱ���������k��������ֱ��AB������Q��0��-2����
��ii��S��OAB=حS��OQA-S��OQBح=حx1-x2ح����Τ�ﶨ�����ҳ���ʽ�����ö��κ��������ʣ�������á�OAB��������ֵ��
��� �⣺��������Բ��������e=$\frac{c}{a}$=$\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{\sqrt{3}}{2}$����a2=4b2��
��P��2��1��������Բ$\frac{{x}^{2}}{4{b}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$����$\frac{1}{{b}^{2}}+\frac{1}{{b}^{2}}=1$����ã�b2=2����a2=8��
����Բ�ķ���Ϊ��$\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1$��
����i����M��N�ֱ��Ƕ���Ķ˵�ʱ����Ȼֱ��ABΪy�ᣬ������ֱ�߹����㣬�������һ����y���ϣ�
��M��N���Ƕ���Ķ˵�ʱ����ֱ��AB�ķ���Ϊy=kx+t����A��x1��y1����B��x2��y2����
��$\left\{\begin{array}{l}{\frac{{x}^{2}}{8}+\frac{{y}^{2}}{2}=1}\\{y=kx+t}\end{array}\right.$����1+4k2��x2+8ktx+4t2-8=0��
���=16��8k2-t2+2����0��
x1+x2=-$\frac{8kt}{4{k}^{2}+1}$��x1x2=$\frac{4{t}^{2}-8}{4{k}^{2}+1}$��
��ֱ��PA�ķ���Ϊy-1=$\frac{{y}_{1}-1}{{x}_{1}-2}$��x-2����
��y-1=$\frac{k{x}_{1}+t-1}{{x}_{1}-2}$��x-2����
���M������Ϊ��0��$\frac{��1-2k��{x}_{1}-2t}{{x}_{1}-2}$����ͬ����֪��N��0��$\frac{��1-2k��{x}_{2}-2t}{{x}_{2}-2}$����
��$\overrightarrow{OM}$=$\overrightarrow{NO}$����$\frac{��1-2k��{x}_{1}-2t}{{x}_{1}-2}$+$\frac{��1-2k��{x}_{2}-2t}{{x}_{2}-2}$=0��
�����������2-4k��x1x2-��2-4k+2t����x1+x2��+8t=0��
��2-4k����$\frac{4{t}^{2}-8}{4{k}^{2}+1}$-��2-4k+2t����-$\frac{8kt}{4{k}^{2}+1}$��+8t=0��
�����������2t+4��k+��t2+t-2��=0��
���ҽ���t=-2ʱ���������k��������ֱ��AB������Q��0��-2����
��ii���ɣ�i����֪��S��OAB=حS��OQA-S��OQBح=ح$\frac{1}{2}$حOQح•حx1ح-$\frac{1}{2}$حOQح•حx2حح��
=$\frac{1}{2}$��2��حx1-x2ح=حx1-x2ح=$\sqrt{��{x}_{1}+{x}_{2}��^{2}-4{x}_{1}{x}_{2}}$��
$\sqrt{��\frac{16k}{4{k}^{2}+1}��^{2}-4��\frac{8}{4{k}^{2}+1}}$=4$\sqrt{\frac{8{k}^{2}-2}{��4{k}^{2}+1��^{2}}}$��
��4k2+1=u����S��OAB=4$\sqrt{\frac{2u-4}{{u}^{2}}}$��
=4$\sqrt{-��\frac{2}{u}-\frac{1}{2}��^{2}+\frac{1}{4}}$��2��
����$\frac{2}{u}$=$\frac{1}{2}$��u=4����k=��$\frac{\sqrt{3}}{2}$ʱ���Ⱥų�����
���OAB��������ֵ2��
���� ���⿼����Բ�ı����̣�����ֱ������Բ��λ�ù�ϵ������Τ�ﶨ�����ҳ���ʽ��������Բ�뺯����ֵ���ۺ�Ӧ�ã�������������������е��⣮

| A�� | a��b��c | B�� | b��a��c | C�� | b��c��a | D�� | a��c��b |
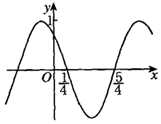 ��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|���У��IJ���ͼ����ͼ��ʾ��������˵��������ǣ�������
��֪����f��x��=Asin����x+�գ���A��0���أ�0��|��|���У��IJ���ͼ����ͼ��ʾ��������˵��������ǣ�������| A�� | ��=�� | |
| B�� | ��=$\frac{��}{4}$ | |
| C�� | f��x���ĵ���������Ϊ��2k-$\frac{1}{4}$��2k+$\frac{3}{4}$����k��Z | |
| D�� | f��x���ĶԳ������ǣ�k+$\frac{1}{4}$��0����k��Z |
 ���д�ͳ�Ļ������ȳ������ӿƽ�Ƶ����ʫ��֪ʶ����Ϊ���ġ��й�ʫ�ʴ�ᡷ��ӫ��������ѧ��ʹ�ѧ��IJ���ѡ�ְ��ɼ���Ϊ���㡢���á�һ�������ȼ���������г�ȡ��100��ѡ�ֽ��е��飬�����Ǹ��ݵ��������Ƶ�ѡ�ֵȼ�����������ͼ��
���д�ͳ�Ļ������ȳ������ӿƽ�Ƶ����ʫ��֪ʶ����Ϊ���ġ��й�ʫ�ʴ�ᡷ��ӫ��������ѧ��ʹ�ѧ��IJ���ѡ�ְ��ɼ���Ϊ���㡢���á�һ�������ȼ���������г�ȡ��100��ѡ�ֽ��е��飬�����Ǹ��ݵ��������Ƶ�ѡ�ֵȼ�����������ͼ����������һ��ȼ������õȼ��ϳ�Ϊ�ϸ�ȼ���������֪������������2��2�����������ݴ��������Ƿ���95%�İ�����Ϊѡ�ֳɼ������㡱���Ļ��̶��йأ�
| ���� | �ϸ� | �ϼ� | |
| ��ѧ�� | |||
| ��ѧ�� | |||
| �ϼ� |
| P��k2��k0�� | 0.10 | 0.05 | 0.005 |
| k0 | 2.706 | 3.841 | 7.879 |
����������ȼ���ѡ����ȡ6�������α��Ϊ1��2��3��4��5��6�������õȼ���ѡ����ȡ6�������α��Ϊ1��2��3��4��5��6����ѡ����6������ȼ���ѡ������ȡһ����������Ϊa����ѡ����6�����õȼ���ѡ������ȡһ����������Ϊb����ʹ�÷�����$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$��Ψһһ��ʵ���⣨x��y���ĸ��ʣ�
| A�� | $\frac{��}{6}$ | B�� | $\frac{��}{3}$ | C�� | $\frac{2��}{3}$ | D�� | $\frac{5��}{6}$ |