题目内容
8.若a为实数,且(2+ai)(a-2i)=4-3i,则a=( )| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
分析 利用复数的运算法则、复数相等即可得出.
解答 解:(2+ai)(a-2i)=4-3i,∴4a+(a2-4)i=4-3i,
∴4a=4,a2-4=-3,解得a=1.
故选:C.
点评 本题考查了复数的运算法则、复数相等,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
19.已知定义在$(0,\frac{π}{2})$上的函数,f′(x)为其导函数,且$\frac{f(x)}{sinx}<\frac{{{f^'}(x)}}{cosx}$恒成立,则( )
| A. | $f(\frac{π}{2})>2f(\frac{π}{6})$ | B. | $\sqrt{3}f(\frac{π}{4})>\sqrt{2}f(\frac{π}{3})$ | C. | $\sqrt{3}f(\frac{π}{6})<f(\frac{π}{3})$ | D. | $f(1)<2f(\frac{π}{6})sin1$ |
20.设a=($\frac{5}{3}$)${\;}^{\frac{1}{6}}$,b=($\frac{3}{5}$)${\;}^{-\frac{1}{5}}$,c=ln$\frac{5}{3}$,则a,b,c的大小关系是( )
| A. | a>b>c | B. | b>a>c | C. | b>c>a | D. | a>c>b |
17.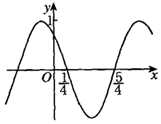 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )| A. | ω=π | |
| B. | φ=$\frac{π}{4}$ | |
| C. | f(x)的单调减区间为(2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z | |
| D. | f(x)的对称中心是(k+$\frac{1}{4}$,0),k∈Z |
1.若无论实数a取何值时,直线ax+y+a+1=0与圆x2+y2-2x-2y+b=0都相交,则实数b的取值范围.( )
| A. | (-∞,2) | B. | (2,+∞) | C. | (-∞,-6) | D. | (-6,+∞) |
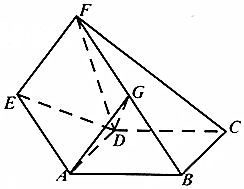 如图,已知矩形ABCD与直角梯形ABFE所在的平面互相垂直,G是BF的中点,∠AEF=∠BFE=90°,且AD=AE=EF=$\frac{1}{2}$FB=1.
如图,已知矩形ABCD与直角梯形ABFE所在的平面互相垂直,G是BF的中点,∠AEF=∠BFE=90°,且AD=AE=EF=$\frac{1}{2}$FB=1.