题目内容
14.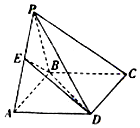 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=2,BC=$\sqrt{2}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=2,BC=$\sqrt{2}$.(1)求证:PC∥平面EBD;
(2)求三棱锥A-PBD的体积.
分析 (1)连接AC,交BD于点O,连接EO,则PC∥EO.由此能证明PC∥平面EBD.
(2)取AB中点H,连接PH,由PA=PB,得PH⊥AB,由VA-PBD=VP-ABD,能求出结果.
解答  证明:(1)连接AC,交BD于点O,连接EO,
证明:(1)连接AC,交BD于点O,连接EO,
则O是AC的中点,
又∵E是PA的中点,∴EO是△PAC的中位线,∴PC∥EO.
又∵EO?平面EBD,PC?平面EBD,
∴PC∥平面EBD.
解:(2)取AB中点H,连接PH,
由PA=PB,得PH⊥AB,
又∵平面PAB⊥平面ABCD,且平面PAB∩平面ABCD=AB,
∴PH⊥平面ABCD.
∵△PAB是边长为2的等边三角形,∴$PH=\sqrt{3}$,
又∵${S_{△ABD}}=\frac{1}{2}×AB×AD=\frac{1}{2}×2×\sqrt{2}=\sqrt{2}$,
∴${V_{三棱锥A-PBD}}={V_{三棱锥P-ABD}}=\frac{1}{3}{S_{△ABD}}•PH=\frac{1}{3}×\sqrt{2}×\sqrt{3}=\frac{{\sqrt{6}}}{3}$.
点评 本题考查线面垂直的证明,考百三棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目