题目内容
3.已知圆M:x2+(y-1)2=1<,Q是x轴上的动点,QA,QB分别切圆M于A,B两点.(1)若Q(1,0),求切线QA,QB的方程;
(2)若|AB|=$\frac{4\sqrt{2}}{3}$,求直线MQ的方程.
分析 (1)设出直线方程,利用直线与圆相切,列出方程求解即可.
(2)设AB与MQ交于P,求出|MP|.在Rt△MBQ中,|MB|2=|MP||MQ|,设Q(x,0),求出Q的坐标,然后求解直线方程.
解答 解(1)设过点Q的圆M的切线方程为x=my+1,则圆心M到切线的距离为1,
∴$\frac{|2m+1|}{\sqrt{{m}^{2}+1}}$=1,∴m=$-\frac{4}{3}$或0,
∴QA,QB的方程分别为3x+4y-3=0和x=1.
(2)设AB与MQ交于P,则MP⊥AB,MB⊥BQ,∴|MP|=$\sqrt{1-(\frac{2\sqrt{2}}{3})^{2}}=\frac{1}{3}$.
在Rt△MBQ中,|MB|2=|MP||MQ|,即1=$\frac{1}{3}$|MQ|,
∴|MQ|=3,∴x2+(y-2)2=9.
设Q(x,0),则x2+22=9,∴x=±$\sqrt{5}$,∴Q(±$\sqrt{5}$,0),
∴MQ的方程为2x+$\sqrt{5}$y-2$\sqrt{5}$=0或2x-$\sqrt{5}$y+2$\sqrt{5}$=0.
点评 本题考查直线与圆的位置关系的应用,考查转化思想以及计算能力.

练习册系列答案
相关题目
13.已知集合A={1,3,$\sqrt{3}$},B={1,m},A∪B=A,则m=( )
| A. | 0或$\sqrt{3}$ | B. | 0或3 | C. | 3或$\sqrt{3}$ | D. | 1或3 |
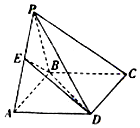 如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=2,BC=$\sqrt{2}$.
如图,四棱锥P-ABCD的底面ABCD是矩形,平面PAB⊥平面ABCD,E是PA的中点,且PA=PB=AB=2,BC=$\sqrt{2}$.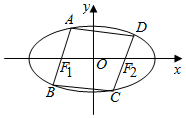 如图所示,椭圆C:$\frac{{x}^{2}}{4}$+y2=1,左右焦点分别记作F1,F2,过F1,F2分别作直线l1,l2交椭圆AB,CD,且l1∥l2.
如图所示,椭圆C:$\frac{{x}^{2}}{4}$+y2=1,左右焦点分别记作F1,F2,过F1,F2分别作直线l1,l2交椭圆AB,CD,且l1∥l2.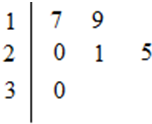 某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.
某车间共有12名工人,随机抽取6名,他们某日加工零件个数的茎叶图如图所示,其中茎为十位数,叶为个位数.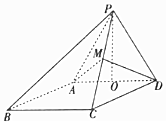 如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.
如图,四棱锥P-ABCD,底面ABCD是∠ABC=60°的菱形,侧面PAD是边长为2的正三角形,O是AD的中点,M为PC的中点.