题目内容
设点P(x,y)是圆(x-3)2+(y-3)2=6上的动点,则
的最大值是 .
| y |
| x |
考点:直线与圆的位置关系
专题:直线与圆
分析:由题意可得
表示圆上的点(x,y)与原点连线的斜率.过原点作圆的切线,设切线方程为y=kx,由圆心到直线的距离等于半径r,求得k的值,可得
的最大值.
| y |
| x |
| y |
| x |
解答:
解:由题意可得
表示圆上的点(x,y)与原点连线的斜率.
过原点作圆的切线,设切线方程为y=kx,即kx-y=0,由圆心到直线的距离等于半径r,
可得
=
,解得 k=3±2
,故
的最大值是 3+2
,
故答案为:3+2
.
| y |
| x |
过原点作圆的切线,设切线方程为y=kx,即kx-y=0,由圆心到直线的距离等于半径r,
可得
| |3k-3| | ||
|
| 6 |
| 2 |
| y |
| x |
| 2 |
故答案为:3+2
| 2 |
点评:本题主要考查直线的斜率公式,直线和圆相切的性质,点到直线的距离公式,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
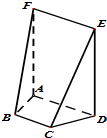 如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=
如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥面ABCD,BC∥AD,CD=1,AD=