题目内容
给定下列命题:
①“x>1”是“x>2”的充分不必要条件;
②“若sinα≠
,则α≠
”;
③若xy=0,则x=0且y=0”的逆否命题;
④命题“?x0∈R,使x02-x0+1≤0”的否定.
其中真命题的序号是 .
①“x>1”是“x>2”的充分不必要条件;
②“若sinα≠
| 1 |
| 2 |
| π |
| 6 |
③若xy=0,则x=0且y=0”的逆否命题;
④命题“?x0∈R,使x02-x0+1≤0”的否定.
其中真命题的序号是
考点:命题的真假判断与应用
专题:简易逻辑
分析:①直接由充分条件、必要条件的概念加以判断;
②找给出的命题的逆否命题,由其逆否命题的真假加以判断;
③由原命题的真假直接判断其逆否命题的真假;
④首先判断给出的特称命题的真假,然后判断其否定的真假.
②找给出的命题的逆否命题,由其逆否命题的真假加以判断;
③由原命题的真假直接判断其逆否命题的真假;
④首先判断给出的特称命题的真假,然后判断其否定的真假.
解答:
解:对于①,
由x>1不能得到x>2,由x>2能得到x>1,
∴“x>1”是“x>2”的必要不充分条件,命题①为假命题;
对于②,
∵“若α=
,则sinα=
”为真命题,
∴其逆否命题“若sinα≠
,则α≠
”为真命题,命题②为真命题;
对于③,
由xy=0,可得x=0或y=0,
∴“若xy=0,则x=0且y=0”为假命题,则其逆否命题为假命题;
对于④,
∵x02-x0+1=(x0-
)2+
>0,
∴命题“?x0∈R,使x02-x0+1≤0”为假命题,则其否定为真命题.
∴真命题的序号是②④.
故答案为:②④.
由x>1不能得到x>2,由x>2能得到x>1,
∴“x>1”是“x>2”的必要不充分条件,命题①为假命题;
对于②,
∵“若α=
| π |
| 6 |
| 1 |
| 2 |
∴其逆否命题“若sinα≠
| 1 |
| 2 |
| π |
| 6 |
对于③,
由xy=0,可得x=0或y=0,
∴“若xy=0,则x=0且y=0”为假命题,则其逆否命题为假命题;
对于④,
∵x02-x0+1=(x0-
| 1 |
| 2 |
| 3 |
| 4 |
∴命题“?x0∈R,使x02-x0+1≤0”为假命题,则其否定为真命题.
∴真命题的序号是②④.
故答案为:②④.
点评:本题考查了命题的真假判断与应用,着重考查原命题与其逆否命题之间的真假关系,考查了命题与命题的否定,是中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
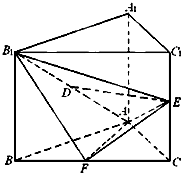 已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.
已知直三棱柱ABC-A1B1C1中,△ABC为等腰直角三角形,∠BAC=90°,且AB=AA1,D、E、F分别为B1A、C1C、BC的中点.