题目内容
在△ABC中，a，b，c分别为角A，B，C的对边，已知∠A=60°，∠B=75°，a=10，则c= ．
考点：正弦定理
专题：计算题
分析：先根据三角形内角和求得C，进而利用正弦定理求得c．
解答：
解：∵∠A=60°，∠B=75°，
∴∠C=180°-60°-75°=45°，
∵a=10，
=
，
即
=
，
∴c=
故答案为：
．
∴∠C=180°-60°-75°=45°，
∵a=10，
| a |
| sinA |
| c |
| sinC |
即
| 10 | ||||
|
| c | ||||
|
∴c=
10
| ||
| 3 |
故答案为：
10
| ||
| 3 |
点评：本题主要考查了正弦定理的运用．考查了学生的基础知识的掌握和计算能力．
练习册系列答案
数学奥赛暑假天天练南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
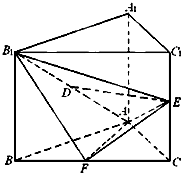已知直三棱柱ABC-A1B1C1中，△ABC为等腰直角三角形，∠BAC=90°，且AB=AA1，D、E、F分别为B1A、C1C、BC的中点．
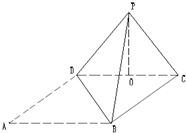矩形ABCD中，AB=6，BC=2直线xcosθ+ysinθ-2=0与圆（x-sinθ）2+（y-2cosθ）2=
（θ∈R）的位置关系为（ ）
| 1 |
| 4 |
| A、相交，相切或相离 |
| B、相切 |
| C、相切或相离 |
| D、相交或相切 |