题目内容

函数y=f（x）在区间（-1，1）上是减函数，且f（1-a）＜f（2a-1），则a的取值范围为（　　）
A、(
2
3
，+∞)
B、(-∞，
2
3
)
C、(0，
2
3
)
D、(
2
3
，1)
考点：函数单调性的性质
专题：函数的性质及应用
分析：根据f（1-a）＜f（2a-1），严格应用函数的单调性．要注意定义域．
解答： 解：∵f（x）在定义域（-1，1）上是减函数，且f（1-a）＜f（2a-1），
∴
-1＜1-a＜1
-1＜2a-1＜1
1-a＞2a-1
，∴0＜a＜
2
3
，
故选：C．
点评：本题主要考查应用单调性解题，一定要注意变量的取值范围．
练习册系列答案
相关题目
已知函数f（x）=loga（1+x），g（x）=loga（1-x），（a＞0，且a≠1）
①判断函数F（x）=f（x）-g（x）的奇偶性，并证明．
②解不等式：F（x）=f（x）-g（x）＞0．
函数f（x）=log
1
2
（x2-x-2）的单调递增区间为
 
．
α是第二象限角，P（x，
5
）为其终边上一点，cosα=
2
4
x，则sinα的值为（　　）
A、
10
4
B、
6
4
C、
2
4
D、-
10
4
过点A（-2，m）和B（m，4）的直线与直线l：x-2y-1=0垂直，则m的值为（　　）
A、10B、2C、0D、-8
满足{a，b}?A⊆{a，b，c，d，e}的集合A有
 
个．
若x
1
3
+x-
1
3
=3，则x+x-1=
 
．
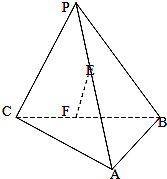如图，E、F分别是三棱锥P-ABC的棱AP、BC的中点，PC=10，AB=6，EF=7，则异面直线AB与PC所成的角为（　　）
A、120°B、45°
C、0°D、60°
为了得到函数y=sin2x的图象，只需要把函数y=sin（2x+
π
6
）的图象（　　）
A、向左平移
π
12
个单位
B、向右平移
π
12
个单位
C、向左平移
π
6
个单位
D、向右平移
π
6
个单位

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网