题目内容
20.已知{an}为等比数列.(1)若an>0,a2a4+2a3a5+a4a6=25,求a3+a5;
(2)若an>0,a5a6=9,求log3a1+log3a2+…+log3a10的值.
分析 (1)由已知式子和等比数列的性质可得a32+2a3a5+a52=25即(a3+a5)2=25,解方程可得;
(2)由题意和等比数列的性质以及对数的运算可得原式=log3(a5a6)5,代值计算可得.
解答 解:(1)∵{an}为等比数列,且an>0,a2a4+2a3a5+a4a6=25,
∴a32+2a3a5+a52=25,故(a3+a5)2=25,解得a3+a5=5;
(2)∵an>0且a5a6=9,
∴log3a1+log3a2+…+log3a10
=log3a1a2…a10=log3(a5a6)5=log395=log3310=10.
点评 本题考查等比数列的通项公式和性质,涉及对数的运算性质,属基础题.

练习册系列答案
 名校通行证有效作业系列答案
名校通行证有效作业系列答案
相关题目
11.“sinα=0”是“cosα=1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
15.已知锐角三角形的边长分别为2,4,x,则x的取值范围是( )
| A. | (1,$\sqrt{5}$) | B. | ($\sqrt{5}$,$\sqrt{13}$) | C. | (1,2$\sqrt{5}$) | D. | (2$\sqrt{3}$,2$\sqrt{5}$) |
5.函数f(x)=asin(2x+φ)+cos(2x+φ),(a>0,|φ|<$\frac{π}{2}$)的最大值为2,且f(-x)=f(x),则a,φ的取值分别为( )
| A. | a=1,φ=$\frac{π}{3}$ | B. | a=1,φ=$\frac{π}{6}$ | C. | a=$\sqrt{3}$,φ=$\frac{π}{3}$ | D. | a=$\sqrt{3}$,φ=$\frac{π}{6}$ |
19.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别是F1,F2,P为椭圆C上的点,在△PF1F2中,点Q满足$\overrightarrow{{F}_{1}P}$=4$\overrightarrow{{F}_{1}Q}$,∠F1PF2=∠QF2F1,则椭圆C的离心率e的取值范围是( )
| A. | 0<e<$\frac{1}{5}$ | B. | $\frac{1}{5}$<e<$\frac{1}{3}$ | C. | $\frac{1}{3}$<e<1 | D. | 0<e<$\frac{1}{5}$或$\frac{1}{3}$<e<1 |
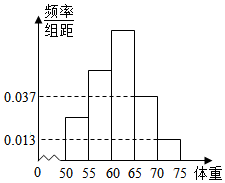 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.