题目内容
8．已知x，y满足约束条件$\left\{\begin{array}{l}{x+y=10}\\{x≥0}\\{y≥0}\end{array}\right.$，则目标函数z=3x+3y的最大值为30，该线性规划有无数个最优解．分析 由x+y=10得z=3（x+y）=30．故z为常数．根据不等式组得解得个数判断最优解的个数．
解答 解：∵x+y=10，∴z=3x+3y=3（x+y）=30．
∵不等式组$\left\{\begin{array}{l}{x+y=10}\\{x≥0}\\{y≥0}\end{array}\right.$有无数组解，
∴该线性规划有无数个最优解．
故答案为：30，无数．
点评 本题考查了不等式组解得个数，简单的线性规划，属于基础题．
练习册系列答案
相关题目
18．如图所示框图，如果输入的n为6，则输出的n2为（ ）
| A． | 16 | B． | 5 | C． | 4 | D． | 25 |
13．下列变换能得到y=cos（x+$\frac{π}{2}$）的图象的有（ ）
①将y=cosx的图象向右平移$\frac{π}{2}$个单位
②将y=cosx的图象向左平移$\frac{π}{2}$个单位
③将y=sinx的图象向右平移π个单位
④将y=sinx的图象向左平移π个单位．
①将y=cosx的图象向右平移$\frac{π}{2}$个单位
②将y=cosx的图象向左平移$\frac{π}{2}$个单位
③将y=sinx的图象向右平移π个单位
④将y=sinx的图象向左平移π个单位．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
7．
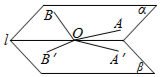如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（ ）
如图，小于90°的二面角α-l-β中O∈l，A，B∈α，且∠AOB为钝角，∠A′OB′是∠AOB在β内的射影，则下列结论一定错误的是（ ）| A． | ∠A′OB′为钝角 | B． | ∠A′OB′＞∠AOB | ||
| C． | ∠AOB+∠AOA′＜π | D． | ∠B′OB+∠BOA+∠AOA′＞π |