题目内容
1.a∈R,设函数f(x)=(-x2+ax)e-x,x∈R.(1)当a=-2时,求函数f(x)的单调减区间;
(2)若x∈(-1,1)内单调递减,求实数a的取值范围.
分析 (1)当a=-2时,f(x)=(-x2-2x)e-x,则f′(x)=(x2-2)e-x,解f′(x)<0,可得函数f(x)的单调减区间;
(2)若x∈(-1,1)内单调递减,则x∈(-1,1)时,f′(x)=[x2-(a+2)x+a]e-x<0恒成立,即x2-(a+2)x+a<0恒成立,进而得到答案.
解答 解:(1)当a=-2时,f(x)=(-x2-2x)e-x,
则f′(x)=(x2-2)e-x,
令f′(x)<0得,x∈(-$\sqrt{2}$,$\sqrt{2}$),
故函数f(x)的单调减区间为(-$\sqrt{2}$,$\sqrt{2}$);
(2)∵函数f(x)=(-x2+ax)e-x,
∴f′(x)=[x2-(a+2)x+a]e-x,
若x∈(-1,1)内单调递减,
则x∈(-1,1)时,x2-(a+2)x+a<0恒成立,
令g(x)=x2-(a+2)x+a,
则g(1)=-1,
故g(-1)≤0,
即1+a+2+a≤0,
解得:a∈(-∞,$-\frac{3}{2}$]
点评 本题考查的知识点是利用导函数研究函数的单调性,转化思想,恒成立问题,难度中档.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
7.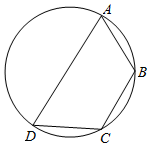 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$ |
13.已知l,m,n为三条不同直线,α,β,γ为三个不同平面,则下列判断正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α∩β=l,m∥α,m∥β,则m∥l | D. | 若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α |
10.过点(3,1)作圆(x-2)2+(y-2)2=4的弦,其中最短的弦长为( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | 4 |
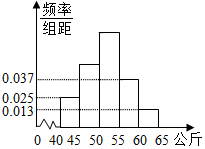 人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.