题目内容
15.已知锐角三角形的边长分别为2,4,x,则x的取值范围是( )| A. | (1,$\sqrt{5}$) | B. | ($\sqrt{5}$,$\sqrt{13}$) | C. | (1,2$\sqrt{5}$) | D. | (2$\sqrt{3}$,2$\sqrt{5}$) |
分析 由余弦定理得出x的不等式组,解不等式组可得.
解答 解:由三角形为锐角三角形可得$\left\{\begin{array}{l}{{2}^{2}+{4}^{2}>{x}^{2}}\\{{2}^{2}+{x}^{2}>{4}^{2}}\\{{x}^{2}+{4}^{2}>{2}^{2}}\end{array}\right.$,
解不等式可得2$\sqrt{3}$<x<2$\sqrt{5}$,
故选:D.
点评 本题考查余弦定理,由余弦定理得出x的不等式组是解决问题的关键,属基础题.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
10.已知等差数列{an}的前n项和为Sn,满足S5=S9,且a1>0.则Sn中最大的是( )
| A. | S6 | B. | S7 | C. | S8 | D. | S15 |
7.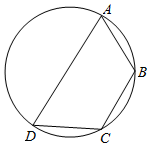 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
 如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )
如图,已知四边形ABCD是圆内接四边形,且∠BCD=120°,AD=2,AB=BC=1,则该四边形的面积等于( )| A. | $\sqrt{3}$ | B. | $\frac{3\sqrt{3}}{4}$ | C. | $\sqrt{3}$+1 | D. | $\frac{\sqrt{3}}{2}$+$\frac{1}{2}$ |
13.已知l,m,n为三条不同直线,α,β,γ为三个不同平面,则下列判断正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α∩β=l,m∥α,m∥β,则m∥l | D. | 若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α |
 已知F1、F2是椭圆C的左右焦点,点A,B为其左右顶点,P为椭圆C上(异于A、B)的一动点,当P点坐标为(1,$\frac{3}{2}$)时,△PF1F2的面积为$\frac{3}{2}$,分别过点A、B、P作椭圆C的切线l1,l2,l,直线l与l1,l2分别交于点R,T.
已知F1、F2是椭圆C的左右焦点,点A,B为其左右顶点,P为椭圆C上(异于A、B)的一动点,当P点坐标为(1,$\frac{3}{2}$)时,△PF1F2的面积为$\frac{3}{2}$,分别过点A、B、P作椭圆C的切线l1,l2,l,直线l与l1,l2分别交于点R,T.