题目内容
18.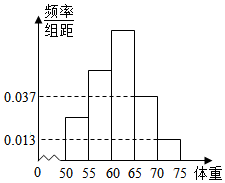 为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.
为了解今年某校高三毕业班准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为12.(Ⅰ)求该校报考飞行员的总人数;
(Ⅱ)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中(人数很多)任选三人,设X表示体重超过60公斤的学生人数,求X的分布列和数学期望.
分析 (Ⅰ)设图中从左到右的前3个小组的频率分别为x,2x,3x,由频率分布直方图的性质求出第2小组的频数为12,频率为2x=0.25,由此能求出该校报考飞行员的总人数.
(Ⅱ)体重超过60公斤的学生的频率为0.625,X的可能取值为0,1,2,3,且X~B(3,0.625),由此能求出X的分布列和数学期望.
解答 解:(Ⅰ)设图中从左到右的前3个小组的频率分别为x,2x,3x,
则x+2x+3x+(0.037+0.013)×5=1,
解得x=0.125,
∵第2小组的频数为12,频率为2x=0.25,
∴该校报考飞行员的总人数为:$\frac{12}{0.25}$=48(人).
(Ⅱ)体重超过60公斤的学生的频率为1-0.125×3=0.625,
∴X的可能取值为0,1,2,3,且X~B(3,0.625),
P(X=0)=${C}_{3}^{0}$(0.375)3=0.052734375,
P(X=1)=${C}_{3}^{1}(0.625)(0.375)^{2}$=0.263671875,
P(X=2)=${C}_{3}^{2}(0.625)^{2}(0.375)$=0.439453125,
P(X=3)=${C}_{3}^{3}(0.625)^{3}$=0.244140625,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | 0.052734375 | 0.263671875 | 0.439453125 | 0.244140625 |
点评 本题考查频率分布直方图的应用,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意二项分布的性质的合理运用.

练习册系列答案
相关题目
13.已知l,m,n为三条不同直线,α,β,γ为三个不同平面,则下列判断正确的是( )
| A. | 若m∥α,n∥α,则m∥n | B. | 若m⊥α,n∥β,α⊥β,则m⊥n | ||
| C. | 若α∩β=l,m∥α,m∥β,则m∥l | D. | 若α∩β=m,α∩γ=n,l⊥m,l⊥n,则l⊥α |
10.过点(3,1)作圆(x-2)2+(y-2)2=4的弦,其中最短的弦长为( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | 4 |
7.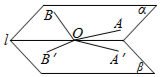 如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )
如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )
 如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )
如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )| A. | ∠A′OB′为钝角 | B. | ∠A′OB′>∠AOB | ||
| C. | ∠AOB+∠AOA′<π | D. | ∠B′OB+∠BOA+∠AOA′>π |
8.为普及学生安全逃生知识与安全防护能力,某学校高一年级举办了安全知识与安全逃生能力竞赛,该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛,现将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
(1)求出上表中的x,y,z,s,p的值;
(2)按规定,预赛成绩不低于90分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为X,求X的分布列和数学期望.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合计 | p | 1 |
(2)按规定,预赛成绩不低于90分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为X,求X的分布列和数学期望.