题目内容
19.设椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别是F1,F2,P为椭圆C上的点,在△PF1F2中,点Q满足$\overrightarrow{{F}_{1}P}$=4$\overrightarrow{{F}_{1}Q}$,∠F1PF2=∠QF2F1,则椭圆C的离心率e的取值范围是( )| A. | 0<e<$\frac{1}{5}$ | B. | $\frac{1}{5}$<e<$\frac{1}{3}$ | C. | $\frac{1}{3}$<e<1 | D. | 0<e<$\frac{1}{5}$或$\frac{1}{3}$<e<1 |
分析 由题意可设|F1Q|=t,|F1P|=4t,运用三角形相似的判断和性质,可得t=c,由椭圆的性质可得a-c<|F1P|<a+c,运用离心率公式计算即可得到所求范围.
解答 解:由点Q满足$\overrightarrow{{F}_{1}P}$=4$\overrightarrow{{F}_{1}Q}$,
设|F1Q|=t,|F1P|=4t,
在△F1PF2和△F1F2Q中,∠F1PF2=∠QF2F1,∠PF1F2=∠F2F1Q,
可得△F1PF2∽△F1F2Q,即有:
$\frac{{F}_{1}P}{{F}_{1}{F}_{2}}$=$\frac{{F}_{1}{F}_{2}}{{F}_{1}Q}$,即$\frac{4t}{2c}$=$\frac{2c}{t}$,
可得t=c,由a-c<|F1P|<a+c,
可得a-c<4c<a+c,
即为a<5c且a>3c,
由e=$\frac{c}{a}$可得$\frac{1}{5}$<e<$\frac{1}{3}$.
故选:B.
点评 本题考查椭圆的离心率的范围,注意运用三角形相似的性质,以及椭圆的点到焦点的距离的最值,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
10.过点(3,1)作圆(x-2)2+(y-2)2=4的弦,其中最短的弦长为( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | 3 | D. | 4 |
7.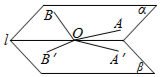 如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )
如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )
 如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )
如图,小于90°的二面角α-l-β中O∈l,A,B∈α,且∠AOB为钝角,∠A′OB′是∠AOB在β内的射影,则下列结论一定错误的是( )| A. | ∠A′OB′为钝角 | B. | ∠A′OB′>∠AOB | ||
| C. | ∠AOB+∠AOA′<π | D. | ∠B′OB+∠BOA+∠AOA′>π |
8.为普及学生安全逃生知识与安全防护能力,某学校高一年级举办了安全知识与安全逃生能力竞赛,该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛,现将所有参赛选手参加笔试的成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.
(1)求出上表中的x,y,z,s,p的值;
(2)按规定,预赛成绩不低于90分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为X,求X的分布列和数学期望.
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合计 | p | 1 |
(2)按规定,预赛成绩不低于90分的选手参加决赛.已知高一(2)班有甲、乙两名同学取得决赛资格,记高一(2)班在决赛中进入前三名的人数为X,求X的分布列和数学期望.
 已知F1、F2是椭圆C的左右焦点,点A,B为其左右顶点,P为椭圆C上(异于A、B)的一动点,当P点坐标为(1,$\frac{3}{2}$)时,△PF1F2的面积为$\frac{3}{2}$,分别过点A、B、P作椭圆C的切线l1,l2,l,直线l与l1,l2分别交于点R,T.
已知F1、F2是椭圆C的左右焦点,点A,B为其左右顶点,P为椭圆C上(异于A、B)的一动点,当P点坐标为(1,$\frac{3}{2}$)时,△PF1F2的面积为$\frac{3}{2}$,分别过点A、B、P作椭圆C的切线l1,l2,l,直线l与l1,l2分别交于点R,T.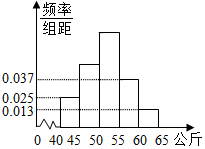 人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.
人的体重是人的身体素质的重要指标之一.某校抽取了高二的部分学生,测出他们的体重(公斤),体重在40公斤至65公斤之间,按体重进行如下分组:第1组[40,45),第2组[45,50),第3组[50,55),第4组[55,60),第5组[60,65],并制成如图所示的频率分布直方图,已知第1组与第3组的频率之比为1:3,第3组的频数为90.