题目内容
7.已知f(t)=log2t,t∈[2,16],对于函数f(t)值域内的任意实数m,则使x2+mx+4>4m+4x恒成立的实数x的取值范围为( )| A. | (-∞,-2$\sqrt{3}$] | B. | [2,+∞) | C. | (-∞,-2$\sqrt{3}$]∪[2$\sqrt{3}$,+∞) | D. | (-∞,-2$\sqrt{3}$)∪(2$\sqrt{3}$,+∞) |
分析 依题意,可得m∈[1,4],x2+mx+4>4m+4x恒成立?(x-4)m+x2-4x+4>0恒成立,构造函数g(m)=(x-4)m+x2-4x+4,则$\left\{\begin{array}{l}{g(1)>0}\\{g(4)>0}\end{array}\right.$,解之即可得到实数x的取值范围.
解答 解:∵t∈[2,16],
∴f(t)=log2t∈[1,4],即m∈[1,4]时,x2+mx+4>4m+4x恒成立,即m∈[1,4],(x-4)m+x2-4x+4>0恒成立,
令g(m)=(x-4)m+x2-4x+4,
则$\left\{\begin{array}{l}{g(1)>0}\\{g(4)>0}\end{array}\right.$,即$\left\{\begin{array}{l}{{x}^{2}-3x>0}\\{{x}^{2}-12>0}\end{array}\right.$,解得:x>2$\sqrt{3}$或x<-2$\sqrt{3}$,
故选:D.
点评 本题考查函数恒成立问题,分离参数m并构造函数g(m)=(x-4)m+x2-4x+4是关键,考查等价转化思想与函数方程思想,属于难题.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
17.已知数列{an}的前n和为Sn,a1=0,an+1=an+2$\sqrt{{a}_{n}+1}$+1,则a5+S4=( )
| A. | 39 | B. | 45 | C. | 50 | D. | 55 |
15.$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$=( )
| A. | -$\frac{99}{100}$ | B. | $\frac{99}{100}$ | C. | -$\frac{100}{99}$ | D. | $\frac{100}{99}$ |
2.方程$\sqrt{{x^2}+{{(y-2)}^2}}+\sqrt{{x^2}+{{(y+2)}^2}}=10$化简的结果是( )
| A. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | B. | $\frac{x^2}{25}+\frac{y^2}{21}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{4}=1$ | D. | $\frac{y^2}{25}+\frac{x^2}{21}=1$ |
17.设集合$A=\left\{{x|\frac{2}{x+1}≥1}\right\}$,集合B={y|y=2x,x<0},则A∪B=( )
| A. | (-1,1] | B. | [-1,1] | C. | (-∞,1] | D. | [-1,+∞) |
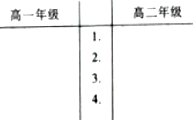 发改委10月19日印发了《中国足球中长期发展规划(2016-2050年)重点任务分工》通知,其中“十三五”校园足球普及行动排名第三,为了调查重庆八中高一高二两个年级对改政策的落实情况,在每个年级随机选取20名足球爱好者,记录改政策发布后他们周平均增加的足球运动时间(单位:h),所得数据如下:
发改委10月19日印发了《中国足球中长期发展规划(2016-2050年)重点任务分工》通知,其中“十三五”校园足球普及行动排名第三,为了调查重庆八中高一高二两个年级对改政策的落实情况,在每个年级随机选取20名足球爱好者,记录改政策发布后他们周平均增加的足球运动时间(单位:h),所得数据如下: