题目内容
下列判断正确的是( )
| A、p:“?x0∈R,2x0≤0”则有?p:不存在x0∈R,2x0>0 | ||||
| B、命题“若x2=1,则x=1”的否命题为:“若x2=1,则x≠1” | ||||
C、?x∈(0,+∞),(
| ||||
| D、设x是实数,则“x>1”是“|x|>1”的充分而不必要条件 |
考点:复合命题的真假
专题:简易逻辑
分析:根据否命题的定义,指数函数与对数函数的取值,充分条件,必要条件的概念即可判断出正确选项.
解答:
解:A.¬p:不存在x0∈R,2x0≤0;
B.否命题应为:若x2≠1,则x≠1;
C.为假命题,∵x=
时,(
)
<1,log
=1,即此时(
)x<log
x;
D.正确,∵x>1能得到|x|>1,而|x|>1,得到x>1,或x<-1,∴不一定得到x>1;
∴x>1是|x|>1的充分而不必要条件.
故选D.
B.否命题应为:若x2≠1,则x≠1;
C.为假命题,∵x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
D.正确,∵x>1能得到|x|>1,而|x|>1,得到x>1,或x<-1,∴不一定得到x>1;
∴x>1是|x|>1的充分而不必要条件.
故选D.
点评:考查否命题的定义,指数函数与对数函数的取值情况或图象,以及充分条件,必要条件的定义.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数f(x)=
sin2x最小值是( )
| 1 |
| 2 |
| A、-1 | ||
B、-
| ||
C、
| ||
| D、1 |
已知x>0,y>0,
+
=1.若x+2y>m2-2m恒成立,则实数m的取值范围是( )
| 2 |
| x |
| 1 |
| y |
| A、m≥4或m≤-2 |
| B、-2<m<4 |
| C、m≥2或m≤-4 |
| D、-4<m<2 |
600°的终边所在的象限为( )
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
已知定义在R上的奇函数f(x)满足f(x+2e)=-f(x)(其中e=2.7182…),且在区间[e,2e]上是减函数,令a=
,b=
,c=
,则f(a),f(b),f(c) 的大小关系(用不等号连接)为( )
| ln2 |
| 2 |
| ln3 |
| 3 |
| ln5 |
| 5 |
| A、f(b)>f(a)>f(c) |
| B、f(b)>f(c)>f(a) |
| C、f(a)>f(b)>f(c) |
| D、f(a)>f(c)>f(b) |
已知实数集合M={x|
+
=1},N={y|y=sinx,x∈M},则M∩N=( )
| x2 |
| 9 |
| y2 |
| 4 |
| A、[-3,3] |
| B、[-1,1] |
| C、(-1,1) |
| D、[-sin3,sin3] |
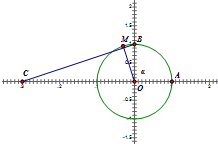 如图,A、B是单位圆与x轴、y轴正半轴的交点,点M在单位圆上,∠AOM=α(0<α<π),点C(-3,0),若BC⊥OM,则sin(2α-
如图,A、B是单位圆与x轴、y轴正半轴的交点,点M在单位圆上,∠AOM=α(0<α<π),点C(-3,0),若BC⊥OM,则sin(2α-| π |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若函数f(x)=sin2x-cos2x+sin2x-m在[0,
]上有零点,则实数m的取值范围为( )
| π |
| 4 |
A、[-1,
| ||
| B、[-1,1] | ||
C、[1,
| ||
D、[-
|