题目内容
1.抛物线顶点在原点,焦点在y轴上,其上一点P(m,1)到焦点的距离为5,则抛物线的标准方程为x2=16y.分析 根据题意,由点P的坐标分析可得抛物线开口向上,设其标准方程为x2=2py,由P到焦点的距离为5,结合抛物线的定义可得1-(-$\frac{p}{2}$)=5,解可得p的值,将p的值代入抛物线方程即可得答案.
解答 解:根据题意,P(m,1)在x轴上方,则抛物线开口向上,
设其标准方程为x2=2py,(p>0)
其准线为y=-$\frac{p}{2}$,
P到焦点的距离为5,则有1-(-$\frac{p}{2}$)=5,
解可得p=8,
则抛物线的标准方程为x2=16y,
故答案为:x2=16y.
点评 本题考查抛物线的简单性质,考查待定系数法的应用,关键是分析抛物线的开口方向,属于中档题.

练习册系列答案
相关题目
12.已知等比数列{an}各项均为正数,公比为q,满足an+1<an,a2a8=6,a4+a6=5,则q2=( )
| A. | $\frac{5}{3}$ | B. | $\frac{4}{9}$ | C. | $\frac{5}{9}$ | D. | $\frac{2}{3}$ |
6.已知数列{an}中,a1=1,前n项和为Sn,且点P(an,an+1)在直线y=x+1上,则$\frac{1}{S_1}+\frac{1}{S_2}+\frac{1}{S_3}+…+\frac{1}{S_n}$=( )
| A. | $\frac{2n}{n+1}$ | B. | $\frac{2}{n(n+1)}$ | C. | $\frac{n(n+1)}{2}$ | D. | $\frac{n}{2(n+1)}$ |
13.如果z 1、z 2∈C且z 1$\overline{{z}_{2}}$=$\overline{{z}_{1}}$z 2≠0,则 $\frac{{z}_{1}}{{z}_{2}}$是( )
| A. | 虚数 | B. | 纯虚数 | C. | 实数 | D. | 不确定 |
10.复数(i-$\frac{1}{i}$)3的虚部是( )
| A. | -8 | B. | -8i | C. | 8 | D. | 8i |
2.用数学归纳法证明1+2+3+4+…++(2n-1)+2n=2n2+n,当n=k+1时左端应在n=k时的基础上加的项是( )
| A. | 2k+1 | B. | 2k+2 | C. | (2k+1)+(2k+2) | D. | 1 |
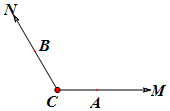 已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.
已知点A,B分别在射线CM,CN(不含端点C)上运动,$∠MCN=\frac{2π}{3}$,在△ABC中,角A,B,C所对的边分别是a,b,c.