题目内容
2.用数学归纳法证明1+2+3+4+…++(2n-1)+2n=2n2+n,当n=k+1时左端应在n=k时的基础上加的项是( )| A. | 2k+1 | B. | 2k+2 | C. | (2k+1)+(2k+2) | D. | 1 |
分析 分别写出n=k和n=k+1时对应的式子,比较两式即可得出结论.
解答 解:n=k时,式子左边为1+2+3+4+…++(2k-1)+2k,
当n=k+1时,式子左边为1+2+3+4+…++(2k-1)+2k+(2k+1)+(2k+2),
故增加的项为(2k+1)+(2k+2),
故选C.
点评 本题考查了数学归纳法,属于基础题.

练习册系列答案
相关题目
2.已知cosα•tanα<0,那么角α是( )
| A. | 第一或第二象限角 | B. | 第二或第三象限角 | ||
| C. | 第三或第四象限角 | D. | 第一或第四象限角 |
10.已知两定点A(-3,0)和B(3,0),动点P(x,y)在直线l:y=-x+5上移动,椭圆C以A,B为焦点且经过点P,则椭圆C的离心率的最大值为( )
| A. | $\frac{{3\sqrt{17}}}{17}$ | B. | $\frac{{3\sqrt{2}}}{5}$ | C. | $\frac{{3\sqrt{17}}}{34}$ | D. | $\frac{{2\sqrt{10}}}{5}$ |
12.复数(1-i)•(1+i)的值是( )
| A. | -2i | B. | 2i | C. | 2 | D. | -2 |
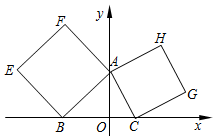 在平面直角坐标系xOy中,已知点A(0,2),B(-2,0),C(1,0),分别以△ABC的边AB、AC向外作正方形ABEF与ACGH,
在平面直角坐标系xOy中,已知点A(0,2),B(-2,0),C(1,0),分别以△ABC的边AB、AC向外作正方形ABEF与ACGH,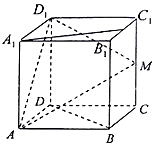 如图边长为2的正方体ABCD-A1B1C1D1中,M、N分别是CC1,B1C1的中点.
如图边长为2的正方体ABCD-A1B1C1D1中,M、N分别是CC1,B1C1的中点.