题目内容
16.已知f(x)=$\left\{\begin{array}{l}{(1-2a)x+5a,x<1}\\{lo{g}_{7}x,x≥1}\end{array}\right.$的值域为R,那么a的取值范围是( )| A. | (-∞,-$\frac{1}{3}$] | B. | (-1,$\frac{1}{2}$) | C. | [-$\frac{1}{3}$,$\frac{1}{2}$) | D. | (0,$\frac{1}{2}$) |
分析 由对数函数的单调性,可得x≥1时,f(x)递增,且有f(x)≥0,由题意可得x<1时,f(x)取得一切的负数,对一次项的系数讨论和端点处的函数值的符号,解不等式即可得到所求范围.
解答 解:由f(x)=$\left\{\begin{array}{l}{(1-2a)x+5a,x<1}\\{lo{g}_{7}x,x≥1}\end{array}\right.$,可得
x≥1时,f(x)递增,且有f(x)≥0,
由题意可得x<1时,f(x)取得一切的负数,
由f(x)=(1-2a)x+5a,x<1,
可得1-2a>0,且1-2a+5a≥0,
即为a<$\frac{1}{2}$,且a≥-$\frac{1}{3}$,即-$\frac{1}{3}$≤a<$\frac{1}{2}$;
当1-2a≤0时,f(x)在x<1不能取得一切的负数.
综上可得a的范围是[-$\frac{1}{3}$,$\frac{1}{2}$).
故选:C.
点评 本题考查函数的值域问题的解法,注意运用对数函数和一次函数的单调性,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
6.若过原点的直线l的倾斜角是直线:y=x的倾斜角的两倍,则l的方程是( )
| A. | y=2x | B. | y=0 | C. | x=0 | D. | y=$\frac{1}{2}$x |
11.已知函数f(x)=x3-12x+8在区间[-3,3]上的最大值与最小值分别为M、m,则$\frac{M}{m}$等于( )
| A. | -24 | B. | -17 | C. | -3 | D. | 3 |
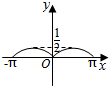
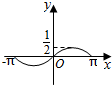
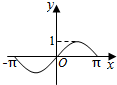
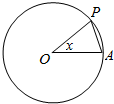 如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )
如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角x的始边为射线OA,终边为射线OP,将△POA的面积表示为x的函数f(x),则y=f(x)在[-π,π]上的图象大致为( )