题目内容
6．
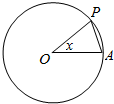如图，圆O的半径为1，A是圆上的定点，P是圆上的动点，角x的始边为射线OA，终边为射线OP，将△POA的面积表示为x的函数f（x），则y=f（x）在[-π，π]上的图象大致为（ ）| A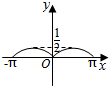． |  | B． |  | C． |  | D． |  |
分析 注意长度、距离为正，再根据三角形的面积公式即可得到f（x）的表达式，然后化简，分析周期和最值，结合图象正确选择
解答 解：在直角三角形OMP中，OP=0A=1，∠POA=x，
∴s△POA=$\frac{1}{2}$×1×1sinx=$\frac{1}{2}$|sinx|，
∴f（x）=$\frac{1}{2}$|sinx|，其周期为T=π，最大值为$\frac{1}{2}$，最小值为0，
故选；A．
点评 本题主要考查三角函数的图象与性质，正确表示函数的表达式是解题的关键，同时考查了三角形的面积公式．
练习册系列答案
备战中考寒假系列答案
相关题目
16．已知f（x）=$\left\{\begin{array}{l}{（1-2a）x+5a，x＜1}\\{lo{g}_{7}x，x≥1}\end{array}\right.$的值域为R，那么a的取值范围是（ ）
| A． | （-∞，-$\frac{1}{3}$] | B． | （-1，$\frac{1}{2}$） | C． | [-$\frac{1}{3}$，$\frac{1}{2}$） | D． | （0，$\frac{1}{2}$） |
17．设m、n是不同的直线，α、β、γ是不同的平的，有以下四个命题：
①若α∥β，α∥γ，则β∥γ ②若α⊥β，m∥α，则m⊥β
③若m∥n，n?α，则m∥α ④若m⊥α，m∥β，则α⊥β
其中正确命题的序号是（ ）
①若α∥β，α∥γ，则β∥γ ②若α⊥β，m∥α，则m⊥β
③若m∥n，n?α，则m∥α ④若m⊥α，m∥β，则α⊥β
其中正确命题的序号是（ ）
| A． | ①③ | B． | ①④ | C． | ②③ | D． | ②④ |
如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则$\underset{lim}{△x→0}$$\frac{f（1+△x）-f（1）}{△x}$=-2（用数字作答）．
16．已知p是“?x＞0，使f（x）=x+$\frac{|a-3|}{x}$的值小于2”的否定．q是“g（x）=ax2-2x在[$\frac{1}{4}$，$\frac{1}{2}$]上单调”，则p是q的（ ）
| A． | 充分不必要 | B． | 必要不充分 | ||
| C． | 充要 | D． | 既不充分也不必要 |